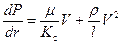 . (9.2.14)
. (9.2.14)
Умножая левую и правую части на плотность  и выражая ее по уравнению состояния реального газа, после интегрирования в соответствующих пределах по Р и r, получаем
и выражая ее по уравнению состояния реального газа, после интегрирования в соответствующих пределах по Р и r, получаем
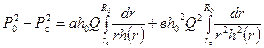 , (9.2.15)
, (9.2.15)
где
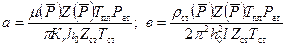 . (9.2.16)
. (9.2.16)
l – коэффициент макрошероховатости, остальные обозначения общепринятые.
Геометрия потока, очевидно, будет определяться функцией h = h (r) в области пространственного потока (см. рис. 9.5). Вся трудность решения состоит в нахождении уравнения кривой h = h (r), ограничивающей область потока, или, другими словами, линии тока. Размер зоны пространственного движения будет зависеть от многих факторов, например, не только от геометрии пласта (R 0 ,h 0 ,b), но и от анизотропии пласта æ;*, дебита Q, градиента давления (grad P) и т. д. Будем аппроксимировать упомянутую линию тока уравнением вида
 . (9.2.17)
. (9.2.17)
Здесь
п=п 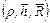 – некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта, и подлежащая определению.
– некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта, и подлежащая определению.
Подставляя (9.2.17) в (9.2.15) и вводя безразмерные параметры
 , (9.2.18)
, (9.2.18)
получаем
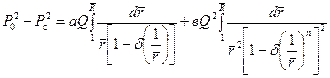 . (9.2.19)
. (9.2.19)
После интегрирования и некоторых преобразований находим окончательно
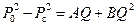 , (9.2.20)
, (9.2.20)
где
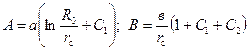 ; (9.2.21)
; (9.2.21)
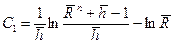 ; (9.2.22)
; (9.2.22)
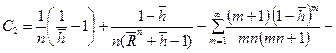
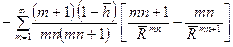 . (9.2.23)
. (9.2.23)
Чтобы определить С 1 и С 2 по формулам (9.2.22) и (9.2.23), необходимо знать значение п. Для нахождения п используем известное решение (9.2.10) для притока к несовершенной по степени вскрытия скважине в однородно-анизотропном пласте при линейном законе фильтрации.
9.2.4. Методика расчета фильтрационных сопротивлений при установившейся фильтрации нефти и газа к несовершенной скважине. Табулирование функций. В газопромысловой практике по данным испытания скважин обычно определяют коэффициенты А и В, входящие в уравнение притока, по которым затем рассчитывается гидропроводность и проницаемость пласта, а также радиус дренирования и коэффициент макрошероховатости. На точность определения указанных параметров, очевидно, существенно будет влиять достоверность определения фильтрационных сопротивлений, обусловленных несовершенством скважины по степени и характеру вскрытия, скин-эффектом призабойной зоны, наличием экрана и конуса подошвенной воды. В связи с этим возникает необходимость уметь рассчитывать указанные функции сопротивления. Был принят следующий порядок расчета на ЭВМ.
а) По формулам (9.2.10) и (9.2.2) рассчитывалась функция сопротивления C 1= f (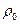 ,
,  ,
,  ). Результаты расчетов затабулированы в широком диапазоне значений параметров: 0,10
). Результаты расчетов затабулированы в широком диапазоне значений параметров: 0,10  10; 0,1
10; 0,1 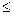

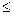 1; 10
1; 10 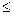

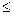 1000 и представлены в таблице (Прил. 1) и графиками [24а]. Из таблиц (Прил. 1) и графиков (рис. 9.6) видно, что добавочные фильтрационные сопротивления С 1, обусловленные частичным вскрытием, возрастают для одних и тех же вскрытий
1000 и представлены в таблице (Прил. 1) и графиками [24а]. Из таблиц (Прил. 1) и графиков (рис. 9.6) видно, что добавочные фильтрационные сопротивления С 1, обусловленные частичным вскрытием, возрастают для одних и тех же вскрытий  при увеличении отношения
при увеличении отношения  или, что то же самое, при увеличении толщины пласта. Особенно резкое увеличение С 1 наблюдается при малых вскрытиях (
или, что то же самое, при увеличении толщины пласта. Особенно резкое увеличение С 1 наблюдается при малых вскрытиях ( <0,4). Отсюда вытекает весьма важный вывод для решения практической инженерной задачи о выборе оптимальной величины вскрытия пласта с подошвенной водой или газовой шапкой. Очевидно, что для пластов большой толщины слишком малые относительные вскрытия окажутся неприемлемы из-за больших фильтрационных сопротивлений.
<0,4). Отсюда вытекает весьма важный вывод для решения практической инженерной задачи о выборе оптимальной величины вскрытия пласта с подошвенной водой или газовой шапкой. Очевидно, что для пластов большой толщины слишком малые относительные вскрытия окажутся неприемлемы из-за больших фильтрационных сопротивлений.
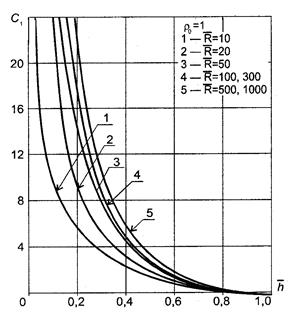
Рис. 9.6. Зависимость коэффициента добавочного фильтрационного сопротивления
С 1 от относительного вскрытия пласта 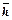 при параметрах ρ;0 и
при параметрах ρ;0 и 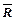
На величину С 1 оказывает существенное влияние степень анизотропности пласта. Из сравнения графиков для разных 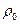 (см. рис. 9.6) видно, что с увеличением анизотропии æ;* или уменьшением параметра
(см. рис. 9.6) видно, что с увеличением анизотропии æ;* или уменьшением параметра 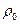 фильтрационные сопротивления возрастают. Это также говорит в пользу того, что в сильно анизотропных пластах с подошвенной водой выбор слишком малых величин вскрытия с целью увеличения безводного периода может оказаться неоправданным.
фильтрационные сопротивления возрастают. Это также говорит в пользу того, что в сильно анизотропных пластах с подошвенной водой выбор слишком малых величин вскрытия с целью увеличения безводного периода может оказаться неоправданным.
б) Из трансцендентного уравнения (9.2.22) при известной теперь функции C 1= f ( ,
,  ,
,  ), рассчитанной по формуле (9.2.10), определялись значения функции п = f (
), рассчитанной по формуле (9.2.10), определялись значения функции п = f ( ,
,  ,
,  ). Результаты расчета затабулированы (Прил. 5 [28]) и представлены графиками (Прил. 6 [28]). Функция п меняется в широком диапазоне: от 0,0017 до 7,44 при изменении параметров
). Результаты расчета затабулированы (Прил. 5 [28]) и представлены графиками (Прил. 6 [28]). Функция п меняется в широком диапазоне: от 0,0017 до 7,44 при изменении параметров  ,
,  и
и  , указанных в пункте (а). При увеличении
, указанных в пункте (а). При увеличении  , уменьшении
, уменьшении  и
и  значения п уменьшаются.
значения п уменьшаются.
в) Функция добавочного фильтрационного сопротивления C 2= f ( ,
,  ,
,  ) рассчитывалась по формуле (9.2.23) c учетом функции п = f (
) рассчитывалась по формуле (9.2.23) c учетом функции п = f ( ,
,  ,
,  ). Результаты табулированы и представлены графически ([24а], Прил. 1). Зависимости C 2= f (
). Результаты табулированы и представлены графически ([24а], Прил. 1). Зависимости C 2= f ( ,
,  ), при параметрах
), при параметрах  [24а] в полулогарифмических координатах оказались линейными, что дает возможность экстраполировать их в сторону
[24а] в полулогарифмических координатах оказались линейными, что дает возможность экстраполировать их в сторону  <0,1 и
<0,1 и  >1. Из графиков видно, что с увеличением анизотропии пласта, т. е. с уменьшением
>1. Из графиков видно, что с увеличением анизотропии пласта, т. е. с уменьшением  , значения С 2 для всех
, значения С 2 для всех  и
и  увеличиваются; для малых
увеличиваются; для малых  и
и  это увеличение происходит более интенсивно. Из представленной зависимости С 2= f (
это увеличение происходит более интенсивно. Из представленной зависимости С 2= f ( ,
,  ) при параметре
) при параметре  (рис. 9.7) видно, что функция фильтрационного сопротивления C 2, обусловленная нелинейным законом фильтрации, с уменьшением параметров
(рис. 9.7) видно, что функция фильтрационного сопротивления C 2, обусловленная нелинейным законом фильтрации, с уменьшением параметров  и
и  изменяется в сторону увеличения более интенсивно. Установленные зависимости C 1= f (
изменяется в сторону увеличения более интенсивно. Установленные зависимости C 1= f ( ,
,  ,
,  ), и C 2= f (
), и C 2= f ( ,
,  ,
,  ), кроме непосредственного их назначения, могут быть использованы для обоснования оптимального интервала вскрытия пласта и установления оптимального режима работы скважин, дренирующих нефтяные, нефтегазовые или газовые залежи с подошвенной водой.
), кроме непосредственного их назначения, могут быть использованы для обоснования оптимального интервала вскрытия пласта и установления оптимального режима работы скважин, дренирующих нефтяные, нефтегазовые или газовые залежи с подошвенной водой.
Для функций равных фильтрационных сопротивлений C 1= f ( ,
,  ,
,  ) и C 2= f (
) и C 2= f ( ,
,  ,
,  ) (табл. 9.2) построена номограмма (рис.9.8). Номограмма окажется полезной для определения предельного относительного вскрытия
) (табл. 9.2) построена номограмма (рис.9.8). Номограмма окажется полезной для определения предельного относительного вскрытия 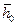 при котором С 1= C 2. Уменьшение относительного вскрытия
при котором С 1= C 2. Уменьшение относительного вскрытия  , т. е.
, т. е.  <
< 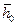 , ведет к резкому увеличению добавочных фильтрационных сопротивлений С 1 и C 2. При
, ведет к резкому увеличению добавочных фильтрационных сопротивлений С 1 и C 2. При  >
> 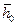 , наблюдается уменьшение С 1 и C 2; при этом соблюдается условие С 1 < C 2, т. е. влияние нелинейного сопротивления становится менее значительным. Отсюда вытекает вывод, что оптимальные относительные вскрытия находятся в области
, наблюдается уменьшение С 1 и C 2; при этом соблюдается условие С 1 < C 2, т. е. влияние нелинейного сопротивления становится менее значительным. Отсюда вытекает вывод, что оптимальные относительные вскрытия находятся в области  >
> 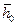 , для которых и следует рассчитывать предельные безводные дебиты.
, для которых и следует рассчитывать предельные безводные дебиты.
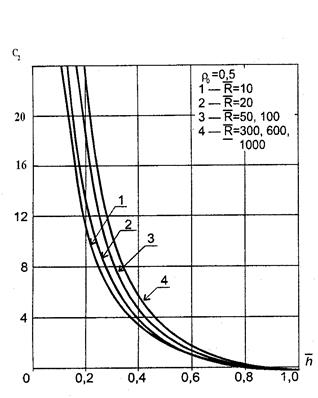
Рис.9.7..Зависимость коэффициента фильтрационного сопротивления С2, обусловленного нелинейным законом движения газа, от относительного вскрытия пласта 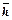 при параметрах ρ;0 и
при параметрах ρ;0 и 
Проанализируем изменение С 2 и С 1 в зависимости от вскрытия пласта  . Примем исходные параметры:
. Примем исходные параметры:  =0,1;
=0,1;  =500. По номограмме (см. рис. 9.8) для заданных параметров находим предельное относительное вскрытие
=500. По номограмме (см. рис. 9.8) для заданных параметров находим предельное относительное вскрытие 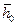 =0,20, которому соответствует С 1=C2=20. При
=0,20, которому соответствует С 1=C2=20. При  =0,1 из таблицы и графиков [24а] находим: С 1=52,38; С 2=95,077. Как видим, фильтрационные сопротивления резко возрастают. При
=0,1 из таблицы и графиков [24а] находим: С 1=52,38; С 2=95,077. Как видим, фильтрационные сопротивления резко возрастают. При  =0,5 имеем: С 1=6,072; С 2=2,964. Следовательно, оптимальные вскрытия, обеспечивающие наименьшие добавочные сопротивления, будут находиться в области
=0,5 имеем: С 1=6,072; С 2=2,964. Следовательно, оптимальные вскрытия, обеспечивающие наименьшие добавочные сопротивления, будут находиться в области  >0,20.
>0,20.
Таблица 9.2
Функции равных фильтрационных сопротивлений С 1( ,
,  ,
,  ) и С 2(
) и С 2( ,
,  ,
,  ); С=С 1 =С 2
); С=С 1 =С 2

| 0,1
| 0,5
| 1,0
|

| 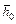
| С
| 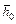
| С
| 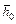
| С
|
|
| 0,58
0,47
0,34
0,29
0,26
0,20
0,19
| 1,60
3,15
7,00
10,50
16,00
20,00
25,50
| 0,65
0,51
0,38
0,30
0,24
0,21
0,20
| 0,80
2,10
5,00
8,70
13,40
17,20
22,00
| 0,76
0,60
0,40
0,34
0,26
0,23
0,20
| 0,20
1,00
3,80
6,00
12,00
15,00
21,00
|
Проиллюстрируем использование таблиц и графиков на конкретном примере. Известно:  =1/ æ;*=1;
=1/ æ;*=1;  =0,1;
=0,1;  =100. Из таблицы [24a] находим С 1
=100. Из таблицы [24a] находим С 1  21,86 и C 2
21,86 и C 2  59,26. Для сравнения расчет произведен также по упрощенным формулам Г.А. Зотова [9, 41] для однородного пласта (
59,26. Для сравнения расчет произведен также по упрощенным формулам Г.А. Зотова [9, 41] для однородного пласта (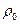 =1). Получено C 1
=1). Получено C 1  18.5 и С2
18.5 и С2  99. Как видим, значения С 1 близки, а значения С 2 существенно отличаются. Отличие, очевидно, объясняется тем, что мы учитываем не только относительное вскрытие и анизотропию, но и геометрию пласта. Для нашего примера функция п
99. Как видим, значения С 1 близки, а значения С 2 существенно отличаются. Отличие, очевидно, объясняется тем, что мы учитываем не только относительное вскрытие и анизотропию, но и геометрию пласта. Для нашего примера функция п  0,0455 (см. §9.2.3)
0,0455 (см. §9.2.3)
Здесь мы не даем сравнения расчетов С 1 с другими методами, поскольку такие сопоставления и оценка точности формулы (9.2.10) приведены в работе [40].
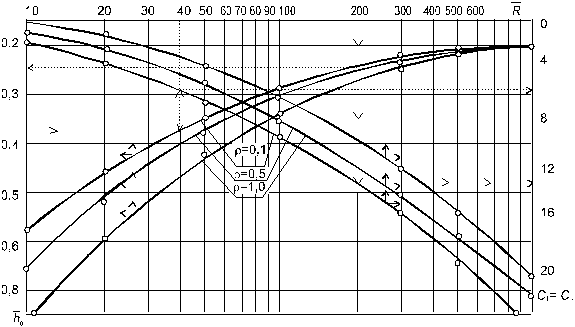
Рис. 9.8. Номограмма равных добавочных фильтрационных
сопротивлений С = С 1 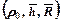 = С 2
= С 2 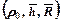

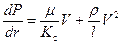 . (9.2.14)
. (9.2.14) и выражая ее по уравнению состояния реального газа, после интегрирования в соответствующих пределах по Р и r, получаем
и выражая ее по уравнению состояния реального газа, после интегрирования в соответствующих пределах по Р и r, получаем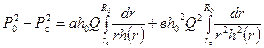 , (9.2.15)
, (9.2.15)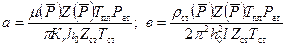 . (9.2.16)
. (9.2.16) . (9.2.17)
. (9.2.17)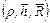 – некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта, и подлежащая определению.
– некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта, и подлежащая определению. , (9.2.18)
, (9.2.18)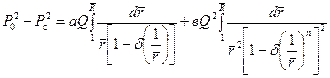 . (9.2.19)
. (9.2.19)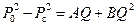 , (9.2.20)
, (9.2.20)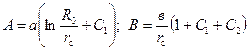 ; (9.2.21)
; (9.2.21)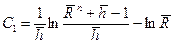 ; (9.2.22)
; (9.2.22)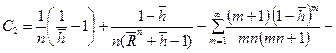
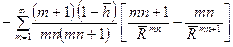 . (9.2.23)
. (9.2.23)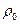 ,
,  ,
,  ). Результаты расчетов затабулированы в широком диапазоне значений параметров: 0,10
). Результаты расчетов затабулированы в широком диапазоне значений параметров: 0,10  10; 0,1
10; 0,1 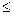

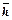 при параметрах ρ;0 и
при параметрах ρ;0 и 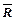
 ,
, 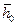 при котором С 1= C 2. Уменьшение относительного вскрытия
при котором С 1= C 2. Уменьшение относительного вскрытия 

 =0,1;
=0,1;  ,
,  ,
,  ) и С 2(
) и С 2(

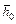
 21,86 и C 2
21,86 и C 2  0,0455 (см. §9.2.3)
0,0455 (см. §9.2.3)
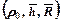 = С 2
= С 2 


