Краткий обзор существующих работ
ПРОСТРАНСТВЕННЫЕ ФИЛЬТРАЦИОНЫЕ ПОТОКИ НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ РЕШЕНИЯ НЕУСТАНОВИВШЕЙСЯ И УСТАНОВИВШЕЙСЯ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ СЖИМАЕМОЙ ЖИДКОСТИ И ГАЗА
Краткий обзор существующих работ Многочисленные работы [1-22 и др.], посвященные задачам пространственной теории фильтрации жидкостей и газов в пористой среде, свидетельствуют о большом практическом интересе к ним при проектировании, разработки и эксплуатации нефтяных, газовых и газоконденсатных месторождений. Сделаем краткий обзор и критический анализ основных работ, относящихся к задачам установившегося и неустановившегося притока пластовой жидкости и газа к гидродинамически несовершенным скважинам. Впервые задача о распределении потенциала скорости фильтрации при установившемся движении в полубесконечном цилиндрическом пласте, частично вскрытом скважиной, была решена М. Маскетом в 1932 году. Затем более детальное исследование этой задачи М. Маскет изложил в своей монографии [1, 1946]. Используя метод отображения, он получил решение для точечного стока в неограниченном пласте с непроницаемой кровлей. Таким же способом П.Я. Полубаринова-Кочина вывела расчетные формулы для дебита наклонной, горизонтальной и вертикальной скважин. Более сложными оказались задачи о распределении потенциала скоростей фильтрации в ограниченном пласте при работе несовершенной скважины. Здесь так же, как и в случае неограниченного пласта, был использован метод отображения стоков (источников) и суперпозиции полей. М. Маскет исследовал также установившийся приток к скважине, несовершенной по степени вскрытия пласта конечной толщины. Применяя метод бесконечного отображения элементарного стока с заданной интенсивностью вдоль линии поглощения (ось вертикальной скважины) относительно непроницаемых кровли и подошвы и суммируя члены для отдельных стоков, после соответствующих преобразований М. Маскет получил приближенное решение о распределении потенциала в пласте. На основе исследований М. Маскета о распределении потенциала в цилиндрическом пласте И.А. Чарный предложил оригинальный метод решения задачи о притоке к несовершенной скважине по двухзонной схеме. Идея И.А. Чарного об условном разделении потока на «зоны» в последствии получила широкое применение при решении многих задач подземной гидрогазодинамики. Производя критический анализ работ, посвященных притоку пластовой жидкости к несовершенной скважине, В.Н. Щелкачев (1949) указывал на необходимость дополнительных теоретических и лабораторных исследований и промысловых испытаний с целью обобщения формул для коэффициента совершенства при притоке однородных жидкостей на случай притока газа и газированных жидкостей. При этом подчеркивалось, что степень и характер совершенства скважины существенно влияют на величину давления на забое. До того времени этот факт исследователями недооценивался. Основы теории притока к несовершенной скважине по характеру вскрытия были заложены М. Маскетом в 1943 году [1]. Затем появляются работы М.И. Тихова [2, 1947] и А.Я. Хейна [3, 1953] в более точной постановке задачи М. Маскета, где формулируется основной закон об оптимальном числе перфораций. В 1954 году А.Л. Хейн разработал теорию установившегося притока жидкости и газа к несовершенной скважине с меридиально-симметричной конструкцией забоя, после чего последовал ряд его же работ, посвященных задачам установившегося и неустановившегося притока жидкости и газа к несовершенным скважинам при линейном и нелинейном законах фильтрации [4]. Новая и наиболее общая математическая постановка задачи о притоке несжимаемой жидкости к скважине, полностью обсаженной и перфорированной, изложена М.Н. Тиховым [2]. Однако эти решения весьма сложны и не доведены до практического применения. Заслуживают внимания решения М.М Глотовского [5] для притока к несовершенной скважине по степени и характеру вскрытия, И.А. Чарного [6] для притока к скважине, обсаженной по всей толщине однородно-анизотропного пласта и перфорированной в верхней части, A.M. Пирвердяна [7] для притока к вертикальной, горизонтальной и наклонной скважинам, Ю.И. Стклянина и А.П. Телкова [8] для несовершенной скважины по степени вскрытия однородно-анизотропного и многослойного пластов. Ряд сложных задач был решен с помощью электромоделирования. Так, В.И. Щуров методом электролитического моделирования исследовал распределение потенциала в пласте, вызванного работой несовершенной скважиной по степени и характеру вскрытия пласта. По данным опытов построена сетка кривых, позволяющая определять величину фильтрационного сопротивления. За последнее время появились работы, в которых рассматриваются вопросы определения коэффициента совершенства, влияние частичного вскрытия пласта и скин-эффекта на кривую восстановления забойного давления и продуктивность скважины; предлагаются наиболее эффективные методы определения фильтрационных сопротивлений, обусловленных несовершенством скважин [9-12]. Во всех указанных работах рассматривались задачи установившегося притока однородной несжимаемой жидкости и газа в недеформируемом однородном или однородно-анизотропном пласте по линейному закону фильтрации к несовершенной скважине. В принципе задача об установившемся притоке жидкости и газа к несовершенной скважине разработана достаточно удовлетворительно. В более общей постановке задача о притоке однородной или «фиктивной» жидкости к несовершенной скважине могла быть сформулирована следующим образом: на внешнем контуре задается некоторая функция; на непроницаемых кровле и подошве – ее производная, равная нулю; в перфорированной части – известная функция, в неперфорированной – ее производная, равная нулю. Требуется найти распределение функции (давление, потенциал, функция Лейбензона, функция Христиановича) в пласте. В точной постановке – это задача Гильберта-Римана, аналитическое решение которой для данного случая пока не получено. Еще большие трудности встречают задачи неустановившегося притока жидкости и газа к гидродинамически несовершенным скважинам. Насколько нам известно, эти задачи рассматривались ограниченным кругом авторов. Обширные исследования неустановившегося притока жидкости и газа к гидродинамически несовершенным по характеру вскрытия пласта скважинам впервые были проведены А.Л. Хейном [3, 4]. Для притока жидкости и газа к несовершенным скважинам по степени вскрытия известны работы М.Т. Абасова и К.Н. Джалилова [13], Е.М. Минского [14], Ю.И, Стклянина [8], Ю.И. Максимова [15], У.П. Куванышева [16], R.G. Nisle [17]. В.Н. Щелкачев и С.Н. Назаров предложили простую приближенную методику учета обеих видов несовершенства скважин и изменения проницаемости в призабойной зоне в условиях упругого режима пласта |18, 19]. E.С. Казарина впервые рассмотрела задачи о притоке к гидродинамически несовершенным круговой и прямолинейной галереям и объемной полосе стоков [20]. Однако широкого практического применения некоторые из указанных решений не получили, хотя они и имеют неоспоримый теоретический интерес. В частности, они не могут быть использованы при обработке кривых нарастания (падения) забойного давления, поскольку их нельзя представить прямолинейной анаморфозой. В связи с этим в основу гидродинамических методов исследования несовершенных скважин и интерпретации результатов положены аналитические решения уравнения пьезопроводности для гидродинамически совершенных скважин, в которые искусственным путем вводятся дополнительные фильтрационные сопротивления, обусловленные несовершенством скважины по степени и характеру вскрытия пласта. Причем фильтрационные сопротивления по степени вскрытия берутся из решений для установившегося притока к совершенной скважине. До сих пор указанные допущения в подземной гидрогазодинамике никем не исследовались даже для условий однородного пласта. В работе С.Г. Каменецкого и др. [21] получены точные, но громоздкие решения неустановившегося притока жидкости к совершенной скважине конечного радиуса, дренирующий бесконечный по протяженности однородный пласт. При этом предполагалось, что в начальный момент имеет место установившаяся фильтрация и распределение давления в пласте удовлетворяет уравнению Лапласа. Для изменения давления в пласте при переменном дебите решение получено в виде интеграла Дюамеля. В работе приведена также формула для притока жидкости к забою при произвольном изменении забойного давления. С помощью функции Грина М. Маскет [1] решил задачу о распределении потенциала (плотности) в бесконечном по протяженности пласте, вызванным синхронно работающими с суммарным дебитом линейными стоками, расположенными непрерывно по окружности. Аналогичная задача для кольца стоков (источников), т. е. для укрупненной скважины, решена И.А. Чарным [22]. Мы рассмотрим задачи неустановившегося притока сжимаемой жидкости (газа) к точечному источнику (стоку) в пространстве, к линии стоков (источников), кольцевому стоку и несовершенной скважине в ограниченном и бесконечном по протяженности и конечном по толщине однородно-анизотропных пластах и взаимодействие скважин при постоянных и переменных дебитах. Закон фильтрации примем линейным.
8.2. Построение обобщенного дифференциального уравнения неустановившейся фильтрации однородной жидкости и газа в пористой среде при изотермическом процессе Дифференциальные уравнения движения сжимаемой однородной жидкости и газа при установившемся неустановившемся изотермическом процессах хорошо известны. Ниже дается упрощенный вывод обобщенного дифференциального уравнения движения, из которого получается ряд уравнений для частных случаев. Кроме того, указаны методы решения и пути использования их в нефтегазопромысловой практике.
8.2.1. Неустановившееся изотермическое движение сжимаемой жидкости в деформируемой пористой среде. Неизвестными функциями являются: давление Уравнение неразрывности записывается в виде
Уравнение состояния для упругой жидкости и пористости суть:
Здесь r 0 и т 0–плотность и коэффициент пористости при начальном давлении Р 0; β;ж и b с – коэффициенты сжимаемости жидкости и скелета пористой среды. Введем обобщенную функцию и продифференцируем ее:
С учетом (8.2.2) и (8.2.3) уравнение (8.2.1) принимает вид
Здесь b* – коэффициент упругоемкости пласта. Рассмотрим некоторые частные случаи. 1. Движение плоскорадиальное неустановившееся, жидкость вязкая упруго-капельная, пласт однородный: r(Р)=r 0= const; m(Р)=m = const; Ki(P)=K = const. Из уравнения (8.2.4) следует известное уравнение пьезопроводности
Здесь æ; – коэффициент пьезопроводности пласта. 2. Движение неустановившееся, плоскорадиальное, пласт однородно-анизотропный (Кr/Кz). Уравнение (8.2.4) принимает вид
æ;* – коэффициент анизотропии пласта. 3. Движение установившееся, жидкость несжимаемая: r(Р)=r 0=const; дР/dt= 0. Из уравнения (8.2.4) следует известное уравнение Лапласа 4. Движение неустановившееся, жидкость упруго-капельная, вязкопластичная, r(Р)=r 0= const. Коэффициент подвижности K / m есть [23]
где К 0 и m 0 – параметры для вязкопластичной жидкости с ослабленными структурно-механическими свойствами, т. е. когда создаваемый градиент сдвига достиг второго начального предельного градиента (grad P ++) [23]. С учетом выражений (8.2.3) и (8.2.7) уравнение (8.2.4) запишется в виде
Для функции (10.2.7) предложены различного вида аппроксимации. Б.И. Султанов для вязкопластичной жидкости предложил соотношение
где
Р 0 – предельное давление сдвига; Р и Р с – пластовое и забойное давление. Взяв производную функцию
Как видим, уравнение (8.2.10) нелинейное и требует численного интегрирования. Линеаризация этого уравнения, очевидно, возможна при режиме пласта
Нетрудно видеть, что при Для установившегося движения из уравнения (8.2.8) следует уравнение Лапласа для функции
8.2.2. Изотермическая фильтрация реального газа. Принимается: температура пласта постоянной, Т = const; коэффициент сверхсжимаемости газа Z=Z (P,T); коэффициент вязкости m=m(Р,Т); коэффициенты проницаемости K = const и пористости т 0= const. Тогда, учитывая уравнение состояния реального газа и обобщенную функцию (8.2.3), из уравнения неразрывности (8.2.1) получаем
Преобразуя уравнение (8.2.12) с учетом дифференциала dР, находим
Нелинейное уравнение (8.2.13) является основным дифференциальным уравнением фильтрации газа и носит название обобщенное уравнение Лейбензона. Одним из методов решения подобных уравнений является метод линеаризации, широко освещенный в литературе [6 и др.]. Если усреднить
Получили нелинейное дифференциальное уравнение Лейбензона для фильтрации идеального газа, аналогичное уравнению Буссинеска. Разделив левую и правую части уравнения (8.2.14) на удельный объемный вес
где Н – напор; С – коэффициент фильтрации; У – высота положения. Уравнение (8.2.15) носит название дифференциального уравнения гидравлической теории нестационарного безнапорного притока Буссинеска. Одним из методов решения подобных уравнений является метод линеаризации Лейбензона [6]. В связи с открытием месторождений природного газа, в смеси которого содержится большое количество кислых компонентов, таких как сероводород, углекислый газ, азот, возникает необходимость учета реальных свойств газа при обработке КВД и определении параметров пласта. С учетом реальных свойств газа для случая Ki = K = const функцию
где
m см – коэффициент динамической вязкости смеси природного газа в атмосферных условиях; m 0 – поправка на вязкость за счет содержания компонентов; α; – поправка на сжимаемость газа, учитывающая содержание в смеси кислых компонентов. Имея опытные данные для определения коэффициентов вязкости и сверхсжимаемости, можно рассчитать функцию (8.2.16). Результаты таких расчетов путем численного интегрирования функции J 0 приведены в диапазоне параметров:
8.2.3. Фильтрация газоконденсатной смеси. Для гомогенной жидкости уравнения (8.2.8) записываются в виде:
где
Н * – потенциальная функция Лейбензона-Христиановича; K к (s) и K г (s) – фазовые проницаемости для конденсата и газа, как функции конденсатонасыщенности s; m к; m г – коэффициенты абсолютной вязкости конденсата и газа в пластовых условиях; r см – плотность газоконденсатной смеси в пластовых условиях; s г – насыщенность пористой среды газом; В к и В г – объемные коэффициенты фаз; a гк – коэффициент растворимости газа в конденсате;
Уравнения (8.2.8), (8.2.10), (8.2.13), (8.2.14) и (8.2.15) могут быть записаны в цилиндрических координатах по аналогии с уравнением (8.2.6).
8.2.4. Обобщение уравнений. Неустановившийся приток к несовершенной скважине. Анализируя приведенные уравнения можно заметить, что структура и методы решения их одинаковы. Это позволяет обобщить их в одно уравнение для однородной «фиктивной» жидкости с некоторой «фиктивной» потенциальной функцией Ф. Тогда, согласно В.Н. Щелкачеву [25], обобщенное уравнение фильтрации может быть записано в унифицированной форме
Отсюда следует: а) при a =0, x = Х и j =0 — уравнение для прямолинейного одномерного потока
б) при a =1, x = r и j =1 — уравнение притока в цилиндрических координатах
в) при a =2, x = r и j =0 — уравнение для сферического потока
Как известно [8], в области, содержащей стоки (источники), потенциал j удовлетворяет уравнению Пуассона Dj=Y (x,y,z,t), где D – оператор Лапласа, Y – плотность стока. Тогда для потенциала точечного стока можно использовать уравнение (8.2.21), добавив в левую часть слагаемое:
где q 0 – интенсивность стока; d (r) – функция Дирака [8]; q (t) – некоторая функция времени. Для притока к точечному стоку с координатами r =0, z=h, расположенному в круговом осессиметричном однородно-анизотропном пласте конечного радиуса, уравнение (8.2.23) с учетом (8.2.25) записывается в виде
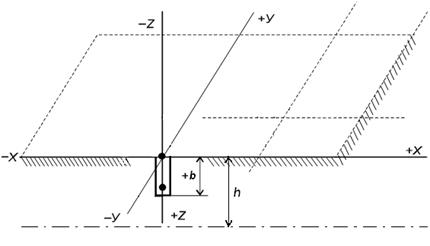
Решения приведенных уравнений широко освещены в задачах подземной гидрогазодинамики и теории разработки нефтяных, газовых и газоконденсатных месторождений для плоского течения. Здесь мы покажем использование полученных уравнений для решения задач неустановившейся пространственной фильтрации жидкости на основе теории потенциала точечного стока-источника. Для линии стоков, частично вскрывающей (несовершенная скважина по степени вскрытия) бесконечный по протяженности однородный пласт в интервале
Рис. 8.1а. Схема притока к несовершенной линии стоков
|

 ; вектор скорости фильтрации
; вектор скорости фильтрации  ; плотность
; плотность 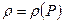 или удельный объемный вес
или удельный объемный вес  ; пористость пласта
; пористость пласта 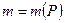 .
.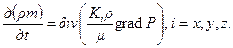 (8.2.1)
(8.2.1)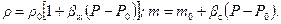 (8.2.2)
(8.2.2)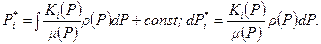 (8.2.3)
(8.2.3)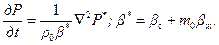 (8.2.4)
(8.2.4)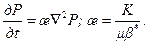 (8.2.5)
(8.2.5)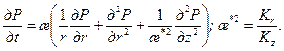 (8.2.6)
(8.2.6)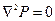 .
.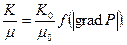 (8.2.7)
(8.2.7)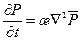 ;
;  ;
; 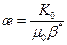 . (8.2.8)
. (8.2.8)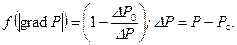 (10.2.9)
(10.2.9)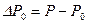 – предельный перепад давления сдвига, определяемый по экспериментальным данным;
– предельный перепад давления сдвига, определяемый по экспериментальным данным;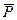 (8.2.8) с учетом выражения (8.2.9), из уравнения (8.2.8) получаем
(8.2.8) с учетом выражения (8.2.9), из уравнения (8.2.8) получаем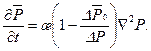 (8.2.10)
(8.2.10)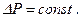 Тогда уравнение (8.2.10) представляет собой уравнение пьезопроводности, решение которого хорошо известно. Переход к давлению после нахождения функции
Тогда уравнение (8.2.10) представляет собой уравнение пьезопроводности, решение которого хорошо известно. Переход к давлению после нахождения функции 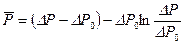 . (8.2.11)
. (8.2.11)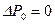 из формулы (8.2.11) следует
из формулы (8.2.11) следует 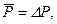 а уравнение (8.2.10) обращается в уравнение пьезопроводности. Предложены также более точные аппроксимации функции (8.2.7), интерпретация которых может быть произведена аналогичным образом [23].
а уравнение (8.2.10) обращается в уравнение пьезопроводности. Предложены также более точные аппроксимации функции (8.2.7), интерпретация которых может быть произведена аналогичным образом [23].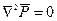 .
.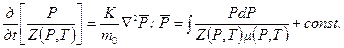 (8.2.12)
(8.2.12) (8.2.13)
(8.2.13)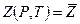 и
и 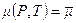 , то из формулы для Р (8.2.12) следует известная функция Лейбензона, подстановка которой в уравнение (8.2.12) дает
, то из формулы для Р (8.2.12) следует известная функция Лейбензона, подстановка которой в уравнение (8.2.12) дает (8.2.14)
(8.2.14)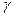 , получаем:
, получаем: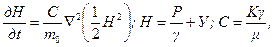 (8.2.15)
(8.2.15)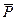 (8.2.12) можно преобразовать к следующему виду:
(8.2.12) можно преобразовать к следующему виду:
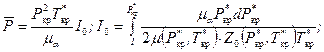 (8.2.16)
(8.2.16)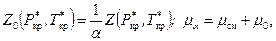 (8.2.17)
(8.2.17)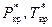 – приведенные критические давление и температура;
– приведенные критические давление и температура;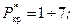
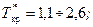 концентрация компонентов (СО 2+ H 2 S)=10¸60% [24, 24а].
концентрация компонентов (СО 2+ H 2 S)=10¸60% [24, 24а].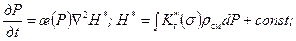 (8.2.18)
(8.2.18)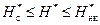 ,
,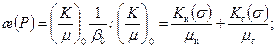 (8.2.19)
(8.2.19)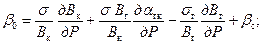 (8.2.20)
(8.2.20)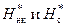 – потенциальные функции, соответствующие давлениям начала конденсации Р нк и на забое скважины Р с.
– потенциальные функции, соответствующие давлениям начала конденсации Р нк и на забое скважины Р с.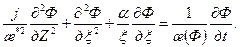 (8.2.21)
(8.2.21)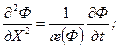 (8.2.22)
(8.2.22)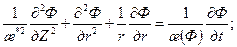 (8.2.23)
(8.2.23)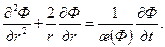 (8.2.24)
(8.2.24)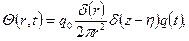 (8.2.25)
(8.2.25)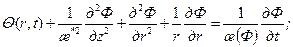 (8.2.26)
(8.2.26)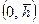 и конечный по толщине h (Рис.8.1а) получено следующее решение для понижения забойного давления в безразмерных параметрах [28]:
и конечный по толщине h (Рис.8.1а) получено следующее решение для понижения забойного давления в безразмерных параметрах [28]: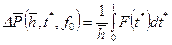 , (8.2.27)
, (8.2.27)