Приток к горизонтальному стволу
Используя известную аппроксимацию, предложенную Ю.П.Борисовым [6], Р.Супрунович и Р.Батлер [31] нашли выражение для падения двления, описываемое формулой (13.5.7). Для нашей задачи с учетом анизотропии æ;* она принимает следующий вид
Авторы [31] решали плоскую задачу фильтрации жидкости к трещине (горизонтальному стволу). Поэтому, строго говоря, использование формулы (13.6.31') для трехмерного пространства будет некорректным. Исходя из сопоставления формул для фильтрационных сопротивлений J тр и J гс, соответствующих притоку к вертикальной трещине и горизонтальному стволу, дренирующих полосообразный полубесконечный пласт, предлагается формула падения давления за счет конвергенции линий тока [6,31]:
где
Здесь
Таким образом, при установившейся фильтрации формула (13.6.9) для горизонтального ствола представится в виде
Рассмотрим конкретный пример для Случая 1, когда f 0>>1. принимаем исходные данные (см.рис.13.2): l 1=50 м; l =2 l 1; h 0=10 м; η;*=0,5; æ;*=5; K =10 мДа=1,02∙10-14м2; μ;=1 мПа·с; ΔР =2∙106 Па; L =100 м; – определяем безразмерные параметры: l *=0,2; ρ;=1,2. – По соответствующим формулам находим: F (ρ;, – Удельный дебит вертикальной трещины, рассчитанные по формуле (13.6.11) для полного вскрытия пласта, т.е. при Полученные результаты дают возможность построить графическую зависимость q 0= q 0(
Рис.13.12. графическая зависимость удельного расхода трещины q 0 от степени вскрытия пласта Заметим, в данном примере q maх=0,88 м2/сут при Расчет, произведенный по формулам (13.6.31') и (13.6.34) при найденных коэффициентах добавочных фильтрационных сопротивлений:
определенных по таблицам (Прил.1) и формуле (9.5.6), дают J вк=7,658 и q 0г=0,337. Как видим, здесь превышение дебита трещины над дебитом горизонтального ствола составляет в 1,31 раза, что явно занижено.
|

 (19.6.31')
(19.6.31')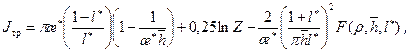 (13.6.32)
(13.6.32) (13.6.33)
(13.6.33) – безразмерная вертикальная ордината положения горизонтального ствола.
– безразмерная вертикальная ордината положения горизонтального ствола.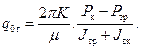 (13.6.34)
(13.6.34) =0,5.
=0,5.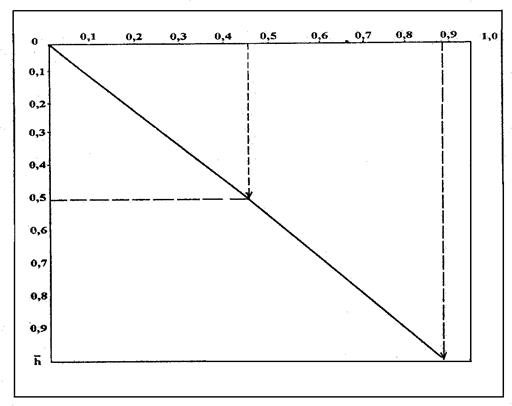
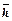
 и
и 



