Расположением горизонтальной скважины
Поскольку ни на подошве, ни на кровле граничные условия не задаются, то авторы [31], строго говоря, решают плоскую задачу в режиме истощения залежи, принимая единичную толщину пласта ( В уравнении (13.5.1) приняты следующие обозначения: Q — дебит скважины, m –коэффициент вязкости, K –проницаемость пласта по горизонтали, А = аb –площадь дренирования, D Р с= Р 0– Р с–депрессия на пласт, Р 0–пластовое давление, Р с–среднее давление на контуре скважины. Приводя уравнение (13.5.1) к безразмерному виду и заменяя его системой конечно-разностных уравнений с использованием пентадиагональной матрицы блока и способа решения, изложенного в книге А. Сеттери и К. Азиза [32], Р. Супрунович и Р. Батлер получили следующую приближенную формулу для расчета наибольшего дебита горизонтального ствола скважины и вертикальной трещины ГРП единичной высоты, соответствующую оптимальным размерам площади дренирования в форме прямоугольника
где
При заданных параметрах А и L оптимальные размеры прямоугольника определяются по формулам:
Итак, в двухмерном пласте горизонтальный ствол рассматривается как линия стока, а в трехмерном пространстве как вертикальная трещина. При этом предполагается, что форма сетки размещения горизонтального ствола остается той же самой. В соответствии с формулой Дюпюи параметр Р* для вертикальной скважины через площадь дренирования А выразится следующей формулой
а эффективность вертикальной трещины определится кратностью отношения
Приток к горизонтальной скважине в трехмерном пространстве подобен притоку к вертикальной трещине, но линии тока при этом должны конвергировать к поверхности скважины, вызывая дополнительное падение давления на преодоление фильтрационного сопротивления, как для вертикальной трещины. Чтобы избежать трудности при непосредственном решении этой задачи численным способом, авторы [31] использовали известную аппроксимацию, предложенную Ю.П. Борисовым. В соответствии с этим было найдено выражение для падения давления за счет вертикальной конвергенции
Теперь дебит горизонтальной скважины будет определяться формулой
Для однородно-анизотропного пласта в формулу (13.5.7) надо ввести коэффициент анизотропии æ;*,т. е. вместо h 0 принять æ;* h 0. Эффективность горизонтального ствола скважины по отношению к вертикальной скважине составит
Эффективность вертикальной трещины по отношению к горизонтальной скважине выражается соотношением
Пример. Приняв исходные параметры: æ;*=3,3; h 0=15 м; площади дренирования А =8; 16; 32 и 64 га; длину горизонтальной скважины L =500 и 200 м, рассчитать оптимальные размеры а и b сетки размещения горизонтальных скважин и сравнительную их эффективность п эф. Расчеты, произведенные по формулам (13.5.3)-(13.5.7), (13.5.10) и (13.5.11), представлены в таблице 13.5.
Таблица 13.5
|

 ) в качестве вертикальной трещины, а в последствии при определении дебита трещины и горизонтальной скважины учитывают как толщину пласта, так и конвергенцию вертикального потока.
) в качестве вертикальной трещины, а в последствии при определении дебита трещины и горизонтальной скважины учитывают как толщину пласта, так и конвергенцию вертикального потока.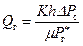 , (13.5.2)
, (13.5.2)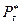 – безразмерныйпараметр, определяемый асимптотическим выражением
– безразмерныйпараметр, определяемый асимптотическим выражением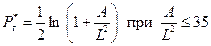 . (13.5.3)
. (13.5.3) . (13.5.4)
. (13.5.4)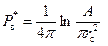 , (13.5.5)
, (13.5.5) . (13.5.6)
. (13.5.6)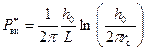 . (13.5.7)
. (13.5.7) . (13.5.8)
. (13.5.8) . (13.5.9)
. (13.5.9)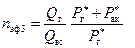 . (13.5.10)
. (13.5.10)


