Залежи с подошвенной водой
Теория конусообразования Маскета-Чарного допускает использование уравнений (13.4.4) и (13.4.5) при возмущенных первоначальных границах раздела ВНК и ГНК. Используя методику определения предельных безводных и безгазовых дебитов для вертикальной скважины, дренирующей нефтегазовую залежь с подошвенной водой и верхним газом (см. §11.3.4), и уравнения (13.4.4) и (13.4.5) можно получить строгое решение аналогичной задачи для горизонтального ствола. Возьмем производные по ординате ξ; потенциалы (13.4.4) и (13.4.5):
Линию, проходящую через точечный сток Чтобы определить предельные безводные и безгазовые дебиты, необходимо знать ординаты – обозначая сумму ряда в уравнении (13.4.4) через – строя графические изображения функции – приравнивая В соответствии с теорией конусообразования Маскета-Чарного потенциал вдоль устойчивой границы раздела двух жидкостей (профиль конуса) изменяется по линейному закону. Для нашего расчетного блока имеем [2,7]:
Решая совместно (13.4.4) и (13.4.8) при
Для определения ординаты Исследование рядов (13.4.1) и (13.4.2) на сходимость дано в работе [4,7] и иллюстрируется табл.13.3 (Δ; – есть отношение остаточного члена ряда к сумме предыдущих). Как видим, степень погрешности формул (13.4.1) и (13.4.2) зависит от параметра ρо и числа принятых членов m в бесконечных рядах. Так при
Таблица 13.3 Погрешность формул (13.4.1) и (13.4.2)
Сравнивая ряды в уравнениях (13.4.1) и (13.4.2) с аналогичными рядами в уравнениях потенциалов для вертикальных скважин [7,30], находим почти их полную аналогию. Отличие заключается в выражениях параметра размещения ρ;. Исходя из равных объемов дренирования для вертикальной скважины и горизонтального ствола πR
где L – длина горизонтального ствола. Для вертикальной скважины выражение для параметра
что дает право использовать полученные результаты для притока к вертикальной скважине применительно к горизонтальному стволу, в особенности, если принять последний как линию стоков. В этом случае в полученных нами уравнениях следует принять В соответствии с изложенным за расчетные предельные удельные дебиты принимаем λ;1 и λ;2 для точечного стока [7,8] дренирующего нефтегазовую залежь с круговым контуром питания, табл. 13.4. В этом случае оптимальное положение скважины стока, обеспечивающее одновременно безводный и безгазовый предельный дебит, определяется соотношением[7,8]
Расчетные значения функции (13.4.12) приведены в табл. 13.4 и представлены графиками, рис. 13.8.
Таблица 13.4
|

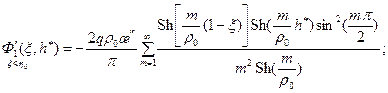 (13.4.6)
(13.4.6) (13.4.7)
(13.4.7) (см. рис. 13.8) параллельно кровле и подошве можно принять за непоницаемую перегородку. Таким образом формально получаем два пласта с толщинами h 1 и h 2. При дренировании верхнего пласта h 1 образуется конус газа, а для нижнего пласта h 2 – конус воды.
(см. рис. 13.8) параллельно кровле и подошве можно принять за непоницаемую перегородку. Таким образом формально получаем два пласта с толщинами h 1 и h 2. При дренировании верхнего пласта h 1 образуется конус газа, а для нижнего пласта h 2 – конус воды.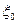 вершин конусов в их предельно-устойчивом состоянии. Сделать можно следующими способами:
вершин конусов в их предельно-устойчивом состоянии. Сделать можно следующими способами: и строя графическое ее изображение как функции
и строя графическое ее изображение как функции 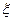 при фиксированных параметрах
при фиксированных параметрах  , методом касательной определить ординату
, методом касательной определить ординату  (см.рис.11.9);
(см.рис.11.9);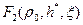 и ее производной
и ее производной 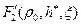 , формула (13.4.7), от ординаты
, формула (13.4.7), от ординаты 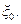
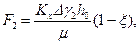
 (13.4.8)
(13.4.8) получаем формулу для безразмерного удельного расхода:
получаем формулу для безразмерного удельного расхода: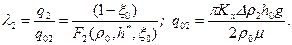 (13.4.9)
(13.4.9)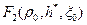 на
на 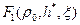 и
и 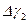 на
на 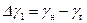 ; минимальный из этих дебитов λ;=min[ λ;1, λ;2] принимается как одновременно предельный безводный и безгазовый.
; минимальный из этих дебитов λ;=min[ λ;1, λ;2] принимается как одновременно предельный безводный и безгазовый.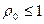 (сильно анизотропные пласты) при m=1 погрешность составляет не более 0,19 %; при m =4 и ρ;0=10 погрешность Δ;=8%. Поэтому для практических расчетов в приведенных рядах при 2< ρ;0≤10 достаточно удержать не более m =4 членов.
(сильно анизотропные пласты) при m=1 погрешность составляет не более 0,19 %; при m =4 и ρ;0=10 погрешность Δ;=8%. Поэтому для практических расчетов в приведенных рядах при 2< ρ;0≤10 достаточно удержать не более m =4 членов. h 0=2
h 0=2 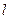 к Lh 0 следует выражение для эквивалентного радиуса нашего расчетного блока
к Lh 0 следует выражение для эквивалентного радиуса нашего расчетного блока (13.4.10)
(13.4.10) . Внося (13.4.10) вместо R к и делая некоторые преобразования, получаем формулу для эквивалентного параметра размещения скважин
. Внося (13.4.10) вместо R к и делая некоторые преобразования, получаем формулу для эквивалентного параметра размещения скважин
 (13.4.11)
(13.4.11) .
.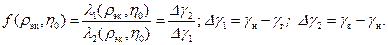 (13.4.12)
(13.4.12)


