Наиболее известные формулы дебита горизонтальных стволов нефтяных скважин при установившемся притоке
Преимущества скважин с горизонтальным стволом наилучшим образом можно понять путем простого анализа работы скважины. Поведение горизонтальной скважины анализируется, когда приток пластовой жидкости происходит по всей длине горизонтального ствола в продуктивном пласте, что отвечает открытому стволу, с хвостовиком, имеющим щелевидные отверстия, или перфорированной колонне с достаточно высокой плотностью их, что позволяет не учитывать добавочные фильтрационные сопротивления за счет перфорации, а также скин-эффект, обусловленный загрязнением призабойной зоны; для выполнения более надежных сравнений необходимо рассматривать как переходный, так и псевдостационарный процессы фильтрации. Это особенно важно для низкопроницаемых коллекторов, в которых продолжительность переходного режима фильтрации очень высока. Однако для достаточно больших периодов работы скважин вполне приемлемо рассмотреть псевдостационарный процесс фильтрации. Приток к горизонтальному стволу скважины в зависимости от его длины можно рассчитать по формуле Джоши [16, 17]:
где
В – объемный коэффициент нефти; L – длина горизонтального ствола; R к – радиус дренирования (условный радиус контура питания). Формула (13.2.1) может быть использована как для расчета дебита, так и для оценки "кратности" увеличения дебита (отношения коэффициентов продуктивности) при сравнении производительности скважин с горизонтальным и вертикальным стволами законченными на один и тот же пласт. Для вертикального ствола, как известно, справедлива формула Дюпюи:
где С 1 – добавочные фильтрационные сопротивления, обусловленные несовершенством вертикальной скважины по степени вскрытия пласта; С 0 – добавочные фильтрационные сопротивления за счет перфорации. Из формул (13.2.1) и (13.2.3) следует отношение коэффициентов продуктивности
Если значения коэффициентов анизотропии æ;*=2÷3 обычные для терригенных коллекторов, что соответствует отношению Отношения коэффициентов продуктивности, определяемые формулой (13.2.4), и дебит, определяемый по формуле (13.2.1), должны сопоставляться с учетом повышенных затрат на бурение скважин с горизонтальными стволами, для чего должны проводитьсяэкономические анализы, например, методом эффективной текущей стоимости. Расчеты по формуле (13.2.1) хорошо согласуются с экспериментальными данными и могут служить при численном моделировании работы горизонтальных стволов эталоном для оценки достоверности формул дебита, связывающих забойное давление и среднее давление в разностном блоке, содержащем горизонтальную скважину [14]. Для расчета дебита горизонтального ствола скважины, расположенного в центре расчетного блока, авторами Фолефак и Арчер [24] предлагают использовать следующую формулу:
где D Х – длина горизонтальной скважины; D Y – ширина расчетного блока; D Z – высота раcчетного блока. По мнению авторов [14] эта формула может быть применена только в случае, когда по толщине пласта рассматривается один расчетный блок. Лучшей формулой для определения эквивалентного радиуса является формула [14, 25]:
Для сравнения приведем формулу дебита горизонтальной скважины В.П. Пилотовского (1964 г.), дренирующей круговой однородный пласт радиуса R к [см.(13.2.1)], где
Renard и Дuрuу [16а] исходят из эллипсоидной области дренирования и предлагают следующую формулу для расчета дебита горизонтального ствола с учетом анизотропии:
где параметр Giger предлагает использовать формулу (13.2.1), где за фильтрационное сопротивление J принимать выражение [16а] J = Gigeг, Reiss и Jouгdan предлагают использовать еще одну формулу [16 а]
|

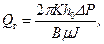 (13.2.1)
(13.2.1) (13.2.2)
(13.2.2) (13.2.3)
(13.2.3)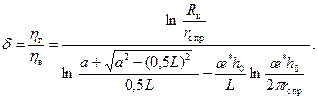 (13.2.4)
(13.2.4) =5÷10, то отношения d невелики. Если же æ;
=5÷10, то отношения d невелики. Если же æ; 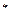 принимают малые значения, что соответствует большим значениям вертикальных проницаемостей, например, в трещиновато-пористых средах или после воздействия на пласт гидроразрывом, то отношения d могут быть существенно большие.
принимают малые значения, что соответствует большим значениям вертикальных проницаемостей, например, в трещиновато-пористых средах или после воздействия на пласт гидроразрывом, то отношения d могут быть существенно большие.
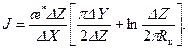 , (13.2.5)
, (13.2.5) . (13.2.6)
. (13.2.6) (13.2.7)
(13.2.7)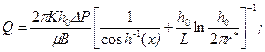 (13.2.8)
(13.2.8) (13.2.9)
(13.2.9)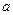 определяется по формуле (13.2.2).
определяется по формуле (13.2.2). (13.2.10)
(13.2.10) (13.2.11)
(13.2.11)


