Определение дебита горизонтального ствола скважины по методу эквивалентных фильтрационных сопротивлений
Приводимая здесь формула дебита горизонтальной скважины достаточно проста и поэтому наглядно показывает влияние на него различных параметров и факторов. Эта формула позволяет проблему конструкции скважины увязывать с другими сложными проблемами разработки нефтяных месторождений. При создании этой формулы авторы [26] использовали известные идеи Ю.П. Борисова и И.А. Чарного, в которых общее фильтрационное сопротивление участка нефтяного пласта со скважиной, математически описываемое сложными специальными функциями, расчленяется на части и представляется последовательностью фильтрационных сопротивлений (именуемых внешними и внутренними), математически описываемых простыми элементарными формулами, поэтому легко анализируемых. Итак, рассматривается прямоугольный участок нефтяной залежи шириной 2 s и длиной т 2 s, который может содержать цепочку из т вертикальных скважин или один горизонтальный ствол длиной l. Цепочка из т вертикальных скважин выделена из равномерной квадратной сетки скважин. Длина горизонтальной части скважины l должна быть заметно меньше длины участка т 2 s. Бурение горизонтальной части скважины может быть осуществлено вместо бурения т вертикальных скважин. Нефтяной пласт обладает эффективной нефтяной толщиной h, проницаемостью k и вязкостью нефти m. На продольных границах этого участка пластовое давление Р пл. По Ю.П. Борисову, дебит цепочки из т вертикальных скважин равен
где
Р пл – пластовое давление; Р сэ– забойное давление добывающих скважин; т – число добывающих скважин; L – расстояние от линии скважин до линии пластового давления, в данном случае L=s, т. е. половине расстояния между соседними рядами вертикальных скважин; 2 s – расстояние между соседними вертикальными скважинами; r с – радиус скважины. Вместо m вертикальных скважин может быть пробурена одна горизонтальная скважина с длиной горизонтальной части l. Дебит этой горизонтальной добывающей скважины составит:
где
L – расстояние от линии горизонтальной скважины до линии пластового давления (принимается L=s). После устранения неопределенности в формуле (13.3.3) при т 2 s = l, сравнение формул (13.3.1) и (13.3.2) в конечном счете дает следующее выражение [26]:
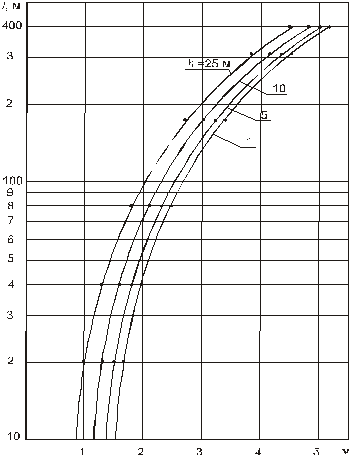
Для условий, когда r с=0,1 м и 2 s =400 м, были сделаны расчеты, результаты которых представлены в табл. 13.1. На рис. 13.3 представлена зависимость отношения коэффициентов продуктивности n горизонтальной и вертикальной скважин, построенная по данным табл. 13.1 при т =1. Указанная зависимость наглядно показывает степень эффективности горизонтальной скважины от длины горизонтального ствола l и толщины продуктивного пласта h 0.
Таблица 13.1
Численные значения n – коэффициента увеличения дебита горизонтального ствола скважины по сравнению с дебитом т вертикальных скважин (по Т.В. Козловой, В.Д. Лысенко)
Развитие идеи Ю.П. Борисова получило в последующей работе В.Д. Лысенко [27], в которой дебит горизонтального ствола в полосообразном пласте длиной L, толщиной h 0, шириной 2 s и длиной горизонтального ствола l <2 sт описывается формулой
В широком диапазоне параметров автор l и h 0 [28] произвел расчет фильтрационных сопротивлений для вертикальных и горизонтальных скважин.
Рис. 13.3. Зависимость коэффициента увеличения дебита
|

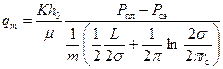 , (13.3.1)
, (13.3.1) – гидропроводность нефтяного пласта;
– гидропроводность нефтяного пласта; , (13.3.2)
, (13.3.2)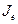 – внешнее фильтрационное сопротивление (по Ю.П. Борисову) есть
– внешнее фильтрационное сопротивление (по Ю.П. Борисову) есть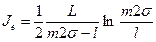 ; (13.3.3)
; (13.3.3)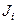 – внутренне фильтрационное сопротивление (по Ю.П. Борисову) есть
– внутренне фильтрационное сопротивление (по Ю.П. Борисову) есть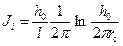 , (13.3.4)
, (13.3.4) . (13.3.5)
. (13.3.5) (13.3.6)
(13.3.6)