Скважине и несовершенной щели в полосообразном пласте
Кровля и подошва (первоначальная граница раздела) считаются непроницаемыми, т. е.
На контуре питания для простоты принимается
Уравнение (13.1.4) с граничными условиями (13.1.5) и (13.1.6) можно решить методом интегральных преобразований, применяя последовательно косинус- и синус-преобразование Фурье с конечными пределами и формулы обращения. Такое решение дано в работах [4, 7]:
Формулы (13.1.7) и (13.1.8) дают распределение потенциала, вызванного точечными стоком или источником, в элементе анизотропного полосообразного пласта. Их можно использовать при экспериментировании на щелевом лотке и для горизонтальной дрены. Если за горизонтальную скважину принять в соответствии с конвергенцией отрезок вертикальной трещины высотой " С ", равной половине длины окружности скважины С = πr c, то потенциал такой трещины (горизонтальной скважины) на единицу ширины потока определится интегралом
Внося (13.1.7) в (13.1.9) и интегрируя, получаем распределение потенциала Ф 1( Потенциал Ф 2 определяем с учетом (13.1.7) и (13.1.8) как
где q – мощность точечного стока (удельный расход жидкости на единицу ширины потока), м2/с. После интегрирования и некоторых преобразований получаем следующую формулу для удельного дебита горизонтальной скважины:
где
Р 0 – среднепластовое давление, Па;
Принимая в уравнениях (13.1.11)-(13.1.13) Заметим, изложенная задача детально рассмотрена в работе [19]. Приведем конкретные примеры: Принимаем следующие иходные данные:
По таблицам [21] определяем значения гиперболических функций, входящих в уравнения (13.1.12) и (13.1.13), и находим J 0= J 1+ J 2=39,43. По формуле (13.1.11) определяем q гс=0,221 м3/сут, что составляет дебит горизонтального ствола длиной L =100 м, Q =0,221∙100=22,1 м3/сут. Для расчета удельного дебита вертикальной трещины формула (13.1.11) остается справедливой, в которой вместо J 0= J 1*– J 2* следует принять
Расчеты удельного расхода по формуле (13.1.11) с учетом J тр=25,19 дают q тр=0,35 м2/сут или Q тр=35 м3/сут. Для сравнения рассчитаем удельный расход для вертикальной скважины в одинаковых условиях. Прежде всего, по исходным параметрам
Принимая исходные данные, находим R к=56,43 м. Для безразмерных параметров:
Внося данные и рассчитанные параметры R к и С 1, получаем Q вс= q вс∙ h 0=0,98∙10=9,8 м3/сут. Сравнивая полученные результаты, видим, что наибольший удельный расход q вс=0,98 м2/сут дает вертикальная скважина в круговом пласте; затем следует вертикальная трещина Q тр=0,35 м2/сут и наименьшее значение q гс=0,22 м2/сут относится к горизонтальному стволу. Однако по дебиту при h 0=10 м и длины горизонтального ствола (вертикальной трещины) L =100 м имеем: Q тр=35 м3/сут; Q гс=22 м3/сут и Q вс=9,8 м3/сут. Очевидно, что столь низкие дебиты горизонтального ствола и трещины ГРП объясняются весьма низкой проницаемостью K =10 мДа=10-14 м2 и малым перепадом давления ΔР =2 МПа. Если, положим, принять K =100 мДа, то дебиты возрастут в 10 раз, т.е. будем иметь: Q тр=350 м3/сут; Q гс=220 м3/сут и Q вс=98 м3/сут. В заключение отметим, приведенные решения могут быть успешно использованы в теории конусообразования для расчета предельных безводных и безгазовых дебитов и депрессий при дренирвании продуктивных пластов горизонтальными стволами и "несовершенными" вертикальными трещинами ГРП, а так же для расчета дебитов. 13.1.2. Решения для установившегося притока жидкости к горизонтальным стволам скважин с круговым контуром питания. В работах В.С Евченко [10, 12] получена формула для расчета дебита горизонтальной скважины
где С г – добавочные фильтрационные сопротивления, обусловленные расположением скважины, длиной скважины, продуктивной толщиной и анизотропией пласта, и определяемые ориентировочно по формулам:
где R к – условный радиус контура питания, определяемый из условия геометрии контура питания и площади дренирования А. При выполнении условия Для перфорированной обсаженной скважины в формулах (13.1.15)-(13.1.18) необходимо учесть добавочные фильтрационные сопротивления С 0 по формуле (1.1.23), т. е. вместо r c принять Для сравнения приведем формулу для определения C г Бузинова-Умрихина [22]
и Пилатовского В.П.
Приведенные формулы дают возможность произвести обработку индикаторных линий и определить параметры пласта для горизонтальных скважин по обычной методике для вертикальных скважин.
13.1.3. Приближенное решение задачи для потенциала горизонтального ствола скважины, дренирующего однродно-анизотропный полубесконечный пласт. Для полубесконечного пласта можно получить наиболее простое приближенное решение задачи, рассмотренной в § 13.1.1, если воспользоваться методом зеркального бесконечного отображения точечного стока (источника) в кровлю и подошву пласта [4]. Многократно отражая скважину-сток с интенсивностью q в кровлю и подошву, получаем две бесконечные цепочки: скважин-стоков и скважин-источников с координатами
С целью получения постоянства потенциала j 0 на контуре l 1, через который проходит ось z, отобразим все скважины полученных двух бесконечных цепочек на ось z и возьмем величину q с обратным знаком. Таким образом, получаются еще две равнодебитные бесконечные цепочки, являющиеся зеркальным отображением первых двух относительно оси z. Результат суперпозиции полей последней пары бесконечных цепочек выражается формулой [4, 7].
Результирующий потенциал, очевидно, запишется в форме
Постоянная интегрирования С определяется из граничного условия: при х =0, j = j 0. Из формулы (13.1.20) следует, что С = j 0. Для однородно-анизотропной среды, где Kх и Kz – проницаемости по горизонтали и вертикали пласта соответственно, требуется решить уравнение фильтрации
Введем новую переменную и характеристику анизотропии æ*:
Тогда уравнение (13.1.21) переходит в обычное уравнение Лапласа для изотропной среды с координатами х, z '
Пласт в новых координатах х, z ', где вертикальные размеры действительного анизотропного пласта изменены в æ;* раз, назовем приведенным однородным пластом. Сравним дебит (на единицу ширины потока) q скважины в однородно-анизотропном пласте с дебитом q ' скважины приведенного пласта
Таким образом, решив задачу для приведенного изотропного пласта, воспользуемся старыми координатами, чтобы получить решение для однородно-анизотропного пласта. Нетрудно видеть, что уравнению (13.1.23) удовлетворяет решение, аналогичное решению (13.1.20), которое с учетом (13.1.22) и (13.1.24) при х = l 1 записывается в безразмерном виде:
где
Если принять за горизонтальную скважину линию стоков с плотностью расхода q на ширину потока по длине горизонтального ствола L, тогда дебит скважины Q = qL, а уравнение (13.1.25) при переходе от потенциала j к давлению Р при x = h * представится в виде:
где
Заметим, уравнение (13.1.25) может быть использовано для расчета предельных безводных (безгазовых) дебитов и депрессий в соответствии с теорией статического конусообразования Маскета-Чарного. Следуя Маскету-Чарному, зону пространственного притока (I) ограничим по длине толщиной пласта h 0 (рис.13.2). Тогда внешняя зона (П) будет характеризоваться размером (l – h 0), где будет иметь место плоскопараллельная фильтрация по толщине пласта. Для ширины потока фильтрация во внешней зоне описывается уравнением
При х =(
При переходе от потенциала к давлению уравнение (13.1.25) для внутренней зоны (I) при
где
Рис.13.2. Схема притока к несовершенной галерее (вертикальной трещине) и горизонтальному стволу в полубесконечном пласте с односторонним контуром питания
Решая совместно (13.1.29) и (13.1.30), находим формулу для удельного расхода горизонтального ствола скважины при двухстороннем контуре питания:
|

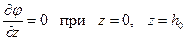 , (13.1.5)
, (13.1.5)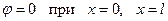 . (13.1.6)
. (13.1.6)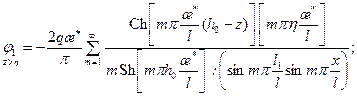 (13.1.7)
(13.1.7)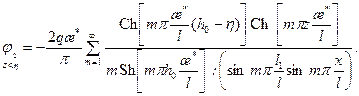 (13.1.8)
(13.1.8)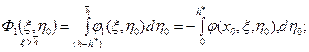
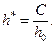 (13.1.9)
(13.1.9)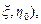 вызванного работой горизонтальной скважины, в интервале
вызванного работой горизонтальной скважины, в интервале 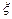 >
> 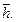
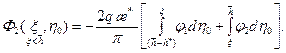 (13.1.10)
(13.1.10)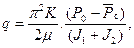 (13.1.11)
(13.1.11)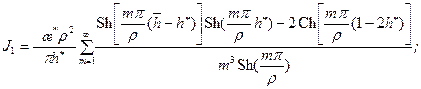 (13.1.12)
(13.1.12)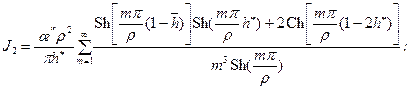 (13.1.13)
(13.1.13)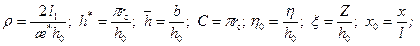
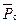 – давление усредненное по стволу скважины или по длине вертикальной трещины, Па.
– давление усредненное по стволу скважины или по длине вертикальной трещины, Па.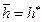 , получм решения для скважины-трещины, расположенной в кровле пласта. При
, получм решения для скважины-трещины, расположенной в кровле пласта. При 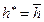 следуют формулы для вертикальной трещины, вскрывшей пласт полностью. Оценка погрешности (Δ;,%) формул (13.1.7) и (13.1.8) показали, что она зависит от параметра ρ и числа принятых членов m в бесконечных рядах. Так при ρ;≤1 (сильно анизотропные пласты) при m=1 погрешность составляет не более 0,19 %; при m =4 и ρ;=10 погрешность Δ;=8 %. Поэтому, для практических расчетов в приведенных рядах достаточно удержать не более четырех членов при ρ;=10.
следуют формулы для вертикальной трещины, вскрывшей пласт полностью. Оценка погрешности (Δ;,%) формул (13.1.7) и (13.1.8) показали, что она зависит от параметра ρ и числа принятых членов m в бесконечных рядах. Так при ρ;≤1 (сильно анизотропные пласты) при m=1 погрешность составляет не более 0,19 %; при m =4 и ρ;=10 погрешность Δ;=8 %. Поэтому, для практических расчетов в приведенных рядах достаточно удержать не более четырех членов при ρ;=10.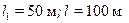 ; h 0=10 м; ρ;=1;
; h 0=10 м; ρ;=1;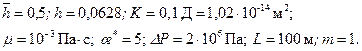
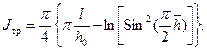 (13.1.14)
(13.1.14)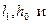 L определим эквивалентный радиус контура питания для круговой залежи, исходя из равенства объемов дренирования вертикальной скважиной и вертикальной трещиной (горизонтальным стволом), т.е. принимаем
L определим эквивалентный радиус контура питания для круговой залежи, исходя из равенства объемов дренирования вертикальной скважиной и вертикальной трещиной (горизонтальным стволом), т.е. принимаем
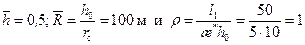 из таблиц (см.Прил.1) находим добавочные фильтрационные сопротивления С 1=4,9. Далее расчет производим по формуле для несовершенной скважины
из таблиц (см.Прил.1) находим добавочные фильтрационные сопротивления С 1=4,9. Далее расчет производим по формуле для несовершенной скважины (13.1.14')
(13.1.14')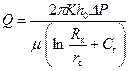 , (13.1.15)
, (13.1.15)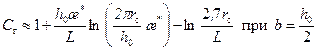 ; (13.1.16)
; (13.1.16)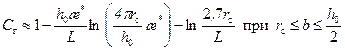 , (13.1.17)
, (13.1.17)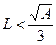 автор [10] рекомендует определять радиус контура питания и для вертикальных скважин.
автор [10] рекомендует определять радиус контура питания и для вертикальных скважин.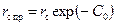 .
.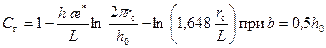 (13.1.16')
(13.1.16')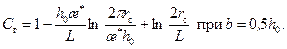 (13.1.17')
(13.1.17')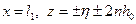 (см. рис. 13.1). Суперпозиция полей двух таких цепочек дает потенциал, который для однородной пористой среды, согласно [4], определится выражением
(см. рис. 13.1). Суперпозиция полей двух таких цепочек дает потенциал, который для однородной пористой среды, согласно [4], определится выражением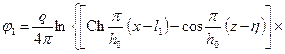
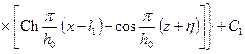 . (13.1.18)
. (13.1.18)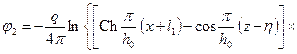
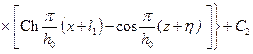 . (13.1.19)
. (13.1.19)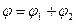 или
или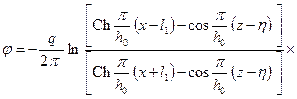
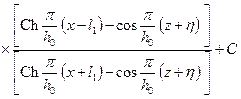 . (13.1.20)
. (13.1.20)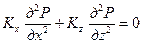 . (13.1.21)
. (13.1.21)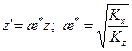 . (13.1.22)
. (13.1.22)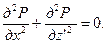 (13.1.23)
(13.1.23)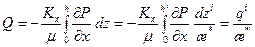 . (13.1.24)
. (13.1.24)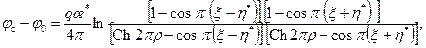 (13.1.25)
(13.1.25)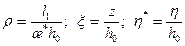 .
.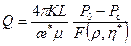 , (13.1.26)
, (13.1.26)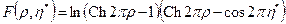 . (13.1.27)
. (13.1.27)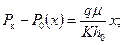 0≤ х ≤(
0≤ х ≤(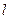 1– h 0). (13.1.28)
1– h 0). (13.1.28)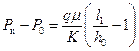 . (13.1.29)
. (13.1.29)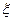 = η;* и давлений Р 0 на контуре
= η;* и давлений Р 0 на контуре  =
= 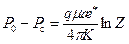 ,
,  (13.1.30)
(13.1.30) . (13.1.31)
. (13.1.31)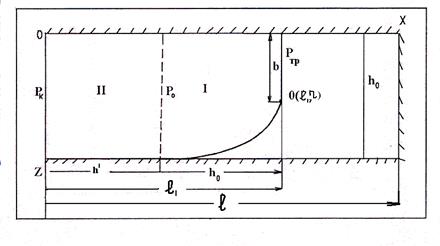
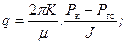
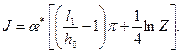 (13.1.32)
(13.1.32)


