Неустановившийся приток жидкости и газа к несовершенной галерее (вертикальной трещине ГРП) и горизонтальному стволу скважины по двухзонной схеме
Рассмотрим одномерное прямолинейно-параллельное движение в обычном пористом пласте. Например, в случае одностороннего притока малосжимаемой жидкости к галерее (см. рис.13.2) давление вдоль пласта распределяется по линейному закону [0≤
где Р к= const – давление на контуре питания; Р 0= Р г – давление на фиктивной галерее; K –коэффициент проницаемости пласта по горизонтали; m – коэффициент абсолютной вязкости жидкости; q – расход на единицу площади сечения пласта, имеющий размерность скорости; l – длина пласта; х –координата. Последующее изложение задачи связано с работой [23]. 1. Случай Р 0= const, В соответствии с работой [37]для нестационарного притока малосжимаемой жидкости в упруго-пористой среде для малых значений t или при
где erfc Z – дополнительный интеграл вероятностей (интеграл Гаусса) [38]; Р 0= const – давление на фиктивной галерее (см. рис. 13.2); æ; – коэффициент пьезопроводности; Р 0(х) – стационарное значение давления. Р( Далее рассмотрим приток к несовершенной галерее (щели) в однородно-анизотропном пласте (см. рис. 13.2). Разделим условно область течения на две зоны [2]: I – зона пространственного движения размером по длине равной толщине пласта h 0;II – зона одномерного плоско-параллельного движения. Галерею примем за линию стоков. Если принять h 0как ширину укрупненной галереи и (l – h 0) как длину пласта, то для течения в зоне II будет справедливо совместное решение (13.6.1) и (13.6.2) при х ≤(l 1– h 0), Р г= Р 0 и при замене длины l на (l – h 0). После ряда преобразований из указанного совместного решения получаем уравнение притока для фиктивной галереи:
где
Полагая в зоне I движение квазиустановившееся [39], используем решение для одностороннего притока к несовершенной галерее (вертикальной трещине) [4,7], которое в соответствии с двухзонной схемой притока в наших обозначениях записывается в виде:
Решение (13.6.5) дает распределение давления (потенциала) в зоне пространственного движения 1 (см. рис.13.2), которое может быть использовано в расчетах предельных безводных и безгазовых дебитов горизонтальных стволов. За расчетное давление на галерее (трещины) примем усредненное его значение вдоль вскрытой толщины пласта
Внося (13.6.5) в (13.6.6) и интегрируя при
где
Решая совместно (13.6.3) и (13.6.7), используя формулу
где
При t →0,
2. Случай Р 0= cоnst, Согласно [37] решение для нестационарного распределения давления в зоне плоскопараллельного движения II с учетом формулы (13.6.2') записывается в виде
На контуре фиктивной галерее
Решая совместно (13.6.1) и (13.6.13), находим
Далее, из совместного решения (13.6.5) и (13.6.14), выражая расход q (t) на единицу площади через удельный расход на единицу ширины трещины при l =2 l 1 (с двухсторонним притоком)
после ряда преобразований получаем расчетную формулу для удельного дебита трещины (13.6.9), в которой фильтрационное сопротивление J тр принимает выражение: где
Если условие этого случая 3. Случай заданного расхода q = q (t) на единицу площади сечения пласта (м/с) Согласно [37] имеем
где
Учитывая, что Р (х, t)= Р 0 – начальное давление на границе зон, для зоны II x =
где
Решая (13.6.18) совместно с (13.6.1), находим
Усредненное давление вдоль трещины как функция времени определится из совместного решения (13.6.7) и (13.6.20), с учетом перехода к удельному расходу, по формуле (13.6.14') уравнением
При
где
Сделаем замену переменных:
Произведем еще раз замену переменных:
С учетом этого интеграл (13.6.24) принимает вид:
Имеется несобственный интеграл [38]
Сравнивая (13.6.25) и (13.6.23) и замечая, что в выражение (13.6.25)
учитывая, что (1–erf Z)=erfc Z, находим
При
или
Внося (13.6.29) в выражение (13.6.27), находим Y (t)=0. Таким образом, при При
где
Таким образом, внося (13.6.30) в уравнение (13.6.21), нетрудно получить формулу удельного расхода q (t) трещины, который при постоянной депрессии ΔР тр= Р к– Р тр= const будет зависеть от фильтрационного сопротивления
где С 1(ρ;,
|

 ≤(l 1– h)]:
≤(l 1– h)]: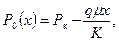 (13.6.1)
(13.6.1)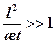 .
.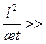 1 имеем следующее решение для распределения давления и формулу дебита:
1 имеем следующее решение для распределения давления и формулу дебита: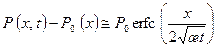 , (13.6.2)
, (13.6.2)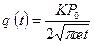 , (13.6.2')
, (13.6.2') = Р 0 – на контуре галереи (l 1– h 0).
= Р 0 – на контуре галереи (l 1– h 0).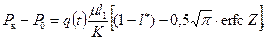 (13.6.3)
(13.6.3)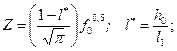
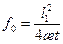 ; (13.6.4)
; (13.6.4)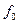 – параметр Фурье.
– параметр Фурье.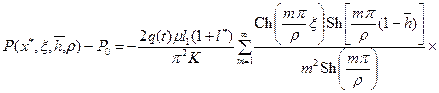
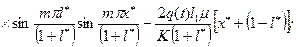 (13.6.5)
(13.6.5)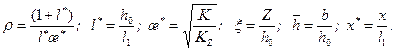
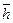 вертикальной трещиной
вертикальной трещиной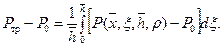 (13.6.6)
(13.6.6)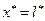 , получаем
, получаем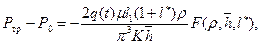 (13.6.7)
(13.6.7)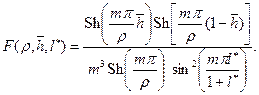 (13.6.8)
(13.6.8)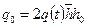 , после ряда преобразований определяем удельный расход жидкости q 0 (м2/с) по вскрытой высоте трещины при двухстороннем контуре питания (l =2 l 1):
, после ряда преобразований определяем удельный расход жидкости q 0 (м2/с) по вскрытой высоте трещины при двухстороннем контуре питания (l =2 l 1):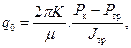 (13.6.9)
(13.6.9)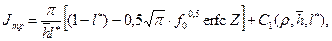 (13.6.10)
(13.6.10)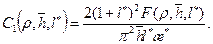 (13.6.10')
(13.6.10')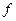 0=∞ имеем еrfс Z =0. Тогда для установившегося притока к "несовершенной" вертикальной трещине второе слагаемое в квадратных скобках формулы (13.6.10) обращается в нуль, а расход на единицу ширины потока q (t)= q 0= const. Eсли трещина вскрывает всю толщину пласта
0=∞ имеем еrfс Z =0. Тогда для установившегося притока к "несовершенной" вертикальной трещине второе слагаемое в квадратных скобках формулы (13.6.10) обращается в нуль, а расход на единицу ширины потока q (t)= q 0= const. Eсли трещина вскрывает всю толщину пласта 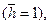 то во всей области х = l 1 имеет место плоскопараллельная фильтрация, а удельный расход, как это следует из (13.6.9) и (13.6.10) определится по формуле
то во всей области х = l 1 имеет место плоскопараллельная фильтрация, а удельный расход, как это следует из (13.6.9) и (13.6.10) определится по формуле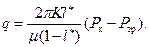 (13.6.11)
(13.6.11)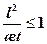 .
.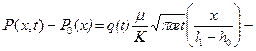
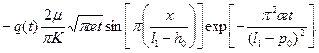 (13.6.12)
(13.6.12)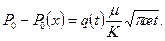 (13.6.13)
(13.6.13)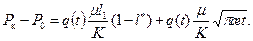
 (13.6.14)
(13.6.14)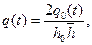 (13.6.14')
(13.6.14')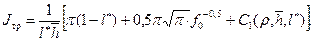 , (13.6.15)
, (13.6.15)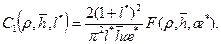 (13.6.15')
(13.6.15')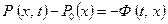 , (13.6.16)
, (13.6.16)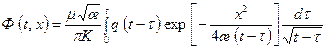 . (13.6.17)
. (13.6.17)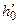 и длине пласта h (l1 – h 0) получаем:
и длине пласта h (l1 – h 0) получаем: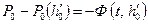 , (13.6.18)
, (13.6.18)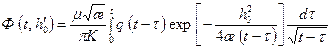 . (13.5.19)
. (13.5.19)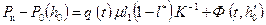 . (13.6.20)
. (13.6.20)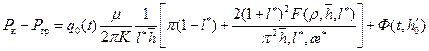 (13.6.21)
(13.6.21)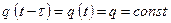 функция (13.6.19) принимает вид:
функция (13.6.19) принимает вид: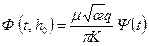 , (13.6.22)
, (13.6.22)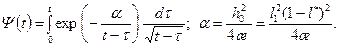 (13.6.23)
(13.6.23)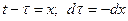 ; пределы меняются: при t =0 следует х = t;при t = t следует х =0. Интеграл преобразуется к виду
; пределы меняются: при t =0 следует х = t;при t = t следует х =0. Интеграл преобразуется к виду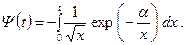 (13.6.24)
(13.6.24)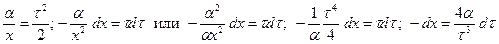 .
.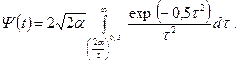 (13.6.25)
(13.6.25)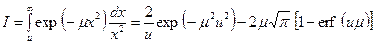 . (13.6.26)
. (13.6.26)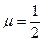 и
и 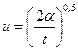 , получаем:
, получаем: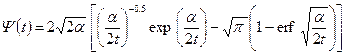 ;
;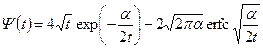 . (13.6.27)
. (13.6.27)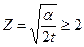 имеем:
имеем: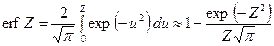 . (13.6.28)
. (13.6.28)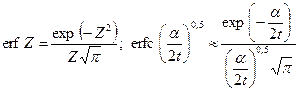 . (13.6.29)
. (13.6.29)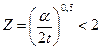 формула (13.6.22), входящая в (13.6.21), с учетом (13.6.27), преобразуется к виду:
формула (13.6.22), входящая в (13.6.21), с учетом (13.6.27), преобразуется к виду: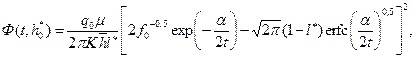 (13.6.30)
(13.6.30)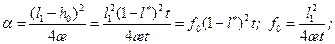
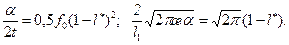
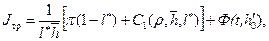 (13.6.31)
(13.6.31)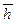 , l *) определяется по формуле (13.6.10'). Для "совершенной" трещины
, l *) определяется по формуле (13.6.10'). Для "совершенной" трещины 


