Радиометра
Задание предполагает статистическую обработку массива данных, на- копленных в ходе контроля стабильности работы радиометра в течение длительного эксперимента, с помощью компьютера. Детектором радио- активного излучения служил галогенный торцевой газоразрядный счетчик, смонтированный в Pb-защите. Режим работы счетчика и электронной части радиометра установлен в соответствии с техническим паспортом. Для эксперимента специально изготовлен точечный источник β-излуче- ния из радионуклида 137Cs (T0,5 = 29,9 г), нанесенного на Al-подложку. Ис- точник герметизирован тонкой полимерной пленкой. Максимальная эне- ргия β-излучения источника равна 0,52 МэВ. На фиксирующей этажерке была выбрана стандартная позиция эталон- ного источника (на расстоянии 1−3 см от окна счетчика) таким образом, чтобы средняя скорость счета была равна ~ 50 отсчет/с. По ходу эксперимента эталон регулярно измеряли по 300 с (сериями по 11 опытов в месяц). Вслед за эталоном контролировали фон радиометра (53 отсчета/300 с). Статисти- ческий анализ массива накопленных данных привел к заключению о высокой стабильности фона в течение эксперимента. Настоящее задание состоит в том, чтобы средствами прикладных ста- тистических программ компьютера (EXEL, ORIGIN) провести обработку массива данных по измерениям эталонного источника и сделать обос- нованное заключение об устойчивости работы радиометра за весь период наблюдения. Поскольку выборочные результаты имеют значения на уровне 1,5 104 отсчетов, все последующие оценки проводятся в рамках статистики Гаусса. Благоприятным фактором оказывается также представительность выборки (k = 132). Получить от преподавателя задание в электронной форме, ввести его в компьютер. Набор данных представлен в виде таблицы, в которой в столбцах приведены выборочные результаты по месяцам для одного года наблюдений. Обработка массива данных проводится в интерактивном режиме.
росов). Для этого найти в столбце максимальное (минимальное) значение сигнала и применить критерий Ni ≥ Наступил момент для введения поправки на распад радионуклида 137Cs. Хотя период полураспада радионуклида велик, при заданной точности измерений падение активности эталона в ходе всего эксперимента надежно фиксируется в процессе статистических оценок. Этой поправкой для дан- ных по одному месяцу можно пренебречь. Проверку гипотезы о стабильности работы радиометра в течение года для скорректированных данных рациональнее проводить с помощью F -кри- терия. Для каждого месяца применить критерий s м2/σ2 ≤ F0.05 где Fp – критическое значение для уровня значимости р = 0,05 при числе степеней свободы f 1 и f 2 (f 1= k – 1, f 2 = ∞). Значение Fp взять из таблиц по статистике. Соблюдение вышеприведенного условия в течение контроли- руемого месяца свидетельствует в пользу вывода о стабильности работы радиометра. В противном случае требуется дополнительный анализ ситуации и техническая проверка радиометра. Проведенная выше проверка направлена на выявления дополнительно- го источника случайной ошибки, что сказывается прежде всего на росте дисперсии массива данных. А изменение параметров отдельных блоков ра- диометра может привести к смещению средней интенсивности сигнала. Выявление систематической погрешности результатов определения прово- дится путем статистической обработки помесячных средних значений по следующему алгоритму. Рассчитать общее среднее значение
И получить дисперсию среднего значения
С помощью критерия
Положим, в исследуемой выборке один результат с наибольшим зна- чением среднего превысил критическое значение t β, f. Это означает, что ги- потезу о смещении среднего для данного месяца с надежностью 5 % сле- дует принять. Естественно, возникает необходимость выяснения причины появления систематической погрешности. В данной работе наиболее ве- роятной причиной может быть старение галогенного газоразрядного счет- чика, следствием которого является увеличение ложных срабатываний (послеимпульсов). Иными словами, эффективность процесса самогашения разряда в процессе эксплуатации счетчика постепенно снижается.
Обработка данных средствами программы EXEL. Ввести массив данных в компьютер. Далее следуют команды: Сервис – Анализ данных – Описательная статистика – Ввести входной интервал (C5:N15) – Ввести выходной интервал (C25:N25) – Итоговая статистика – ОК. Выбрать отдельные строки «Среднее» и «Стандартное» и поместить в соответствующих столбцах исходной таблицы. Провести проверку на выброс. Удалить (заменить) отбракованный результат. Пересчитать данные исправленного столбца в режиме функция. Для средних ввести поправку на распад. Получить откорректирован- ную строку. По этим данным в режиме функция получить общее среднее и дисперсию среднего. Провести проверку на промах, однако его появление на данном этапе обработки маловероятно. В завершение провести проверку средних по месяцам на принад- лежность к одному распределению, используя критерий Стьюдента.
|

 Первоначально надо по каждому месяцу рассчитать среднее значение числа отсчетов (N м) и стандартное отклонение (sм). Проверить стандартное отклонение по критерию s м > 3σ. Когда это условие соблюдается, данные соответствующего столбца требуется проверить на наличие промахов (выб-
Первоначально надо по каждому месяцу рассчитать среднее значение числа отсчетов (N м) и стандартное отклонение (sм). Проверить стандартное отклонение по критерию s м > 3σ. Когда это условие соблюдается, данные соответствующего столбца требуется проверить на наличие промахов (выб-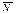 ±3σ. Следует подчеркнуть, что этот критерий здесь уместен по причине большой выборки и принятой кон- цепции о нормальном распределении величин. В противном случае необ- ходимо пользоваться распределением Стьюдента. Если результат, отве- чающий указанному выше критерию, будет обнаружен, он должен быть удален, как промах. Предположим, что других результатов, удовлет- воряющих указанному выше критерию, в этой выборке нет. Тогда расчет среднего и стандартного отклонения по этому столбцу должен быть сделан заново на основе оставшихся аргументов.
±3σ. Следует подчеркнуть, что этот критерий здесь уместен по причине большой выборки и принятой кон- цепции о нормальном распределении величин. В противном случае необ- ходимо пользоваться распределением Стьюдента. Если результат, отве- чающий указанному выше критерию, будет обнаружен, он должен быть удален, как промах. Предположим, что других результатов, удовлет- воряющих указанному выше критерию, в этой выборке нет. Тогда расчет среднего и стандартного отклонения по этому столбцу должен быть сделан заново на основе оставшихся аргументов.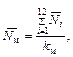 где k м = 12.
где k м = 12.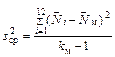
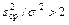 установить наличие (отсутствие) сомнительных величин в наборе средних. Если таковые обнаружены, следует применить статистический критерий, для наибольшего (наименьшего) среднего, используя критерий
установить наличие (отсутствие) сомнительных величин в наборе средних. Если таковые обнаружены, следует применить статистический критерий, для наибольшего (наименьшего) среднего, используя критерий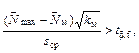 где t β, f - критерий Стьюдента при уровне надежности β для односторонней проверки и числе степеней свободы f = k м – 1. Обычно β принимают равным 0,05 (см. таблицу в Приложении).
где t β, f - критерий Стьюдента при уровне надежности β для односторонней проверки и числе степеней свободы f = k м – 1. Обычно β принимают равным 0,05 (см. таблицу в Приложении).


