Принципы расчета плитных фундаментов на упругом основании
5.11.1 Для расчета плитных фундаментов на упругом основании рекомендуется применять следующие расчетные модели: а) метод местных упругих деформаций; б) метод линейно-деформируемого полупространства; в) метод упругого слоя на несжимаемом основании или с переменным модулем деформации грунта по его глубине. Метод а), как правило, следует применять для слабых, малопрочных оснований, б) и в) — для мало- и среднесжимаемых оснований при расчетах гибких конструкций: балок, лент (в т. ч. перекрестных) и массивных плит. 5.11.2 Фундаменты на упругом основании следует рассчитывать с учетом их гибкости. Балки
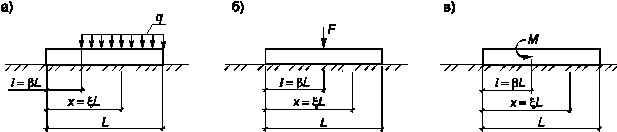
где Е 0 и n0 — соответственно модуль деформации, МПа, и коэффициент Пуассона грунта; Е 1, n1 — модуль упругости, МПа, и коэффициент Пуассона материала фундамента; I — момент инерции поперечного сечения фундамента, м4; l и h — длина и высота фундамента, м; R — радиус плиты, м. 5.11.3 Расчет фундаментов на упругом основании производится в зависимости от модели основания по 5.11.1 и условий его работы численными методами по соответствующим программам, с использованием ПЭВМ, или расчетно-практическими методами по соответствующим таблицам [2]. Расчет плитных фундаментов, загруженных различными нагрузками (рисунок 5.13), с использованием таблиц, производится по показателю гибкости a:
где n — коэффициент поперечных деформаций грунта; Е — модуль деформации грунта, МПа; L и b — длина и ширина балки, м; В — жесткость балки, МПа∙м4. При загружении балки несколькими силами суммарные усилия находят сложением их одноименных ординат. Расчет плитного фундамента на упругом основании приведен в примере Г.7 приложения Г.
Рисунок 5.13 — Схемы загружения балок различными нагрузками: а) равномерно распределенной; б) сосредоточенной;
|

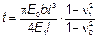 (5.69)
(5.69) (5.70)
(5.70)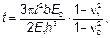 (5.71)
(5.71)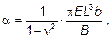 (5.72)
(5.72)