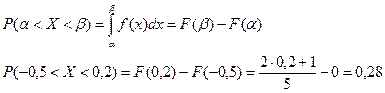Контрольна робота
по курсу «Теорія ймовірностей та мат. аналіз»
Виконав: ст. групи ЕП – 10 3з Давіденко О. В. .
Алчевск, 2011 1. 1. Побудувати інтервальний варіаційний ряд для випадкової величини. Крок обирається за формулою Сетрджеса. 2. Побудувати гістограму і полігон частот. 3. Знайти медіану і моду. 4. Знайти методом добутків вибіркові середнє, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації, асиметрію й ексцес. 5. Знайти довірчий інтервал для математичного сподівання з надійністю u=0,95 (при нормальному розподілі) 6. При рівні значимості а=0,05 за допомогою критерію Пірсона перевірити гіпотезу про нормальний закон розподілу. Вимоги: усі числові характеристики повинні бути записані з відповідними одиницями виміру. Результати вимірів (у мм) п’ятдесяти однотипних деталей дали наступні значення:
Рішення. Формула Стерджеса має вигляд:
де N – число одиниць сукупності.
Величину інтервалу визначають по наступній формулі
1) Складемо таблицю частот згрупованої вибірки:
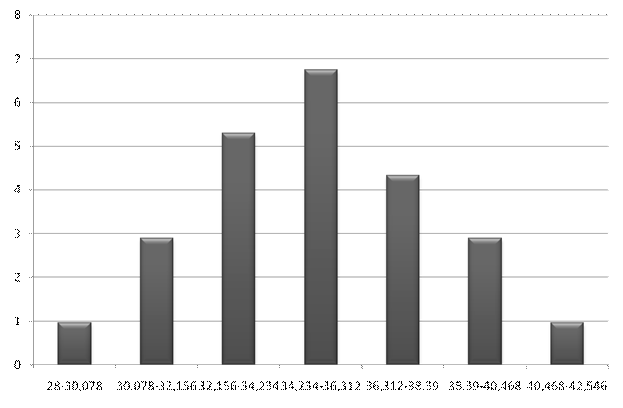
2) Побудуємо гістограму частот:
3) Побудуємо полігон частот
3) Знайдемо медіану і моду інтегральному ряді розподілу Медіана дорівнює:
Мода дорівнює:
4) Знайдемо методом добутків вибіркові середнє, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації, асиметрію й ексцес.
Вибіркове середнє дорівнює:
Складемо заповнимо таблицю:
Обчислимо умовні моменти 1-го і 2-го порядку:
Знайдемо крок h (різниця між сусідніми інтервалами):
Обчислимо шукані, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації, асиметрію й ексцес Дисперсія дорівнює:
Середнє квадратичне відхилення дорівнює:
Коефіцієнт варіації дорівнює:
Асиметрія визначається по формулі:
Ексцес визначимо по формулі
5). Знайти довірчий інтервал для математичного сподівання з надійністю u=0,95 (при нормальному розподілі) Довірчий інтервал для невідомого генерального середнього має вигляд:
Тут всі величини, крім t, відомі. Знайдемо t зі співвідношення u=0,95. За таблицею Лапласа знаходимо t=1,96. Підставивши t=1,96, у=2,88,
6). При рівні значимості а=0,05 за допомогою критерію Пірсона перевірити гіпотезу про нормальний закон розподілу. Для знаходження теоретичних частот використаємо формули:
і скористаємось розрахунковою таблицею
Значення критерію Ксп обчислюється за формулою:
За таблицями критичних точок розподілу
Оскільки Ксп=4,5<6,85=kкр, то гіпотеза про нормальний закон розподілу приймається. 2. 1. За даними досліджень побудувати кореляційне поле 2. За результатами спостережень знайти лінійне рівняння регресії і додати лінію регресії на поле кореляції 3. Обчислити коефіцієнт кореляції 4. Перевірити на значимість вибірковий коефіцієнт кореляції 5. Дати економічний аналіз всіх отриманих результатів. Залежність між кількістю внесених добрів Х (у кг/га) і врожайністю BY (у ц/га).
Використовуючи програму Excel побудуємо кореляційне поле, додамо лінію регресії та визначимо лінійне рівняння регресії на поле кореляції.
Коефіцієнт кореляції для лінійного звязку обчислимо за формулою:
де
σх – середнє квадратичне відхилення ознаки х; σу – середнє квадратичне відхилення ознаки у. Складемо розрахункову таблицю:
3. Пасажир може звернутися за отриманням квитка до однієї з двох кас вокзалу. Ймовірність його звертання до кожної каси залежить від її знаходження та дорівнює відповідно 0,8 та 0,5. Ймовірність того, що на потрібний момент квитків потрібного пасажиру напрямку не буде для першої каси дорівнює 0,7 а для другої – 0,5. Знайти ймовірність того, що пасажир купить потрібний йому квиток. Нехай за умов попередньої задачі відомо, що пасажир купив квиток. Яка ймовірність того що він купив його в першій касі.
Рішення
А = «Пасажир купив потрібний квиток» В1 = «Купив квиток в перший клас» В2 = «Купив квиток в другий клас»
а)
б) Формула Байеса:
4. Дискретну випадкову величину Х задано законом розподілу: а) Х 3 10 15 Р 0,6 0,2 0,2 Знайти функцію розподілу цієї випадкової величини та побудувати її графік. Випадкову величину Х задано функцією розподілу.
Рішення
б)
1. Щільність розподілу ймовірностей:
2.
Вірогідність попадання видадкових величин Х на интервалі
|

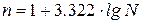



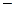 xi+1
xi+1

 /n
/n








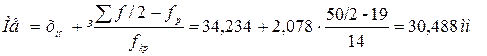

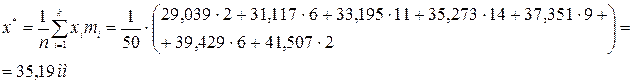
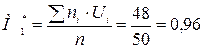
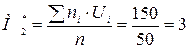
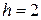

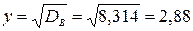
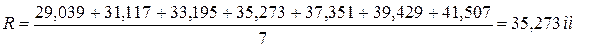




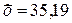 , n=50, остаточно одержимо шуканий довірчий інтервал:
, n=50, остаточно одержимо шуканий довірчий інтервал: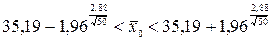


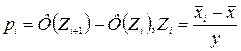
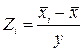
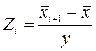


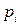


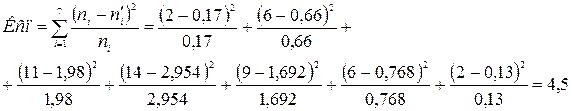
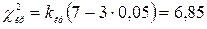
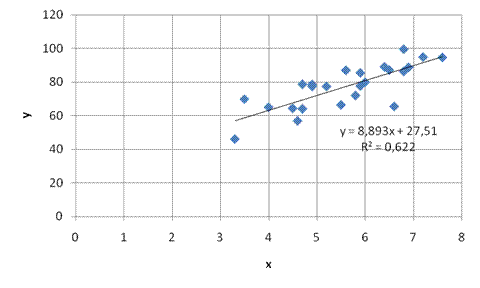
 ,
, – середній добуток ознак х та у;
– середній добуток ознак х та у;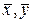 – середнє значення ознаки відповідно х і у;
– середнє значення ознаки відповідно х і у;
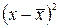
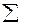
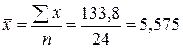
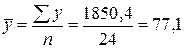

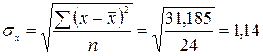

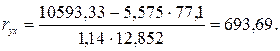
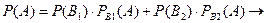 Формула повної ймовірності.
Формула повної ймовірності.
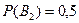


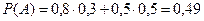
 ймовірність, що куплено квиток в 1 класі.
ймовірність, що куплено квиток в 1 класі.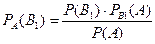
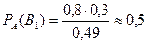

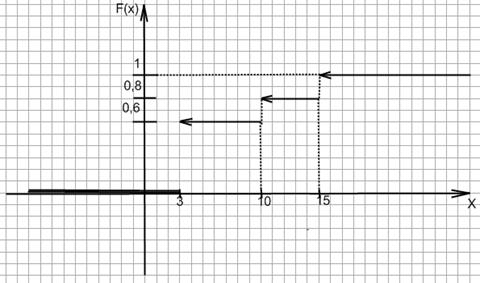 Побудуємо графік.
Побудуємо графік.
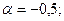


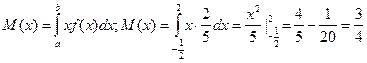

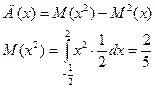
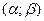 .
.