Проверка статистических гипотез осуществляется на основе данных выборки. Для этого используют специальным образом подобранную случайную величину (выборочную статистику), являющуюся функцией наблюдённых значений, точное или приближённое распределение которой известно.
О. 7.Статистическим критерием (тестом) называют случайную величину К, с помощью которой принимаются решения о принятии или отвержении выдвинутой нулевой гипотезы.
Для проверки нулевых гипотез по выборочным данным вычисляют частные значения входящих в критерий величин и, таким образом, получают частное (наблюдаемое) значение критерия.
О. 8. Проверка гипотезы с помощью статистического критерия значимости есть правило отклонения нулевой гипотезы, заключающееся в разбиении области возможных значений К на две непересекающиеся подобласти, причём нулевая гипотеза отвергается, если наблюдаемое значение критерия К принадлежит критической подобласти, и считается согласующейся с опытом, если наблюдаемое значение критерия К не принадлежит критической подобласти.
50.Ошибки, допускаемые при проверке статистических гипотез
Уровень значимости статистического критерия
О. 1. Ошибкой первого рода называется ошибка отклонения верной нулевой гипотезы 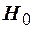 .
.
О. 2. Уровнем значимости статистического критерия называется вероятность  совершения ошибки первого рода.
совершения ошибки первого рода.
Отклонение нулевой 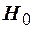 гипотезы при уровне значимости
гипотезы при уровне значимости  означает, что, отклоняя эту гипотезу, мы или не ошибаемся (то есть гипотеза
означает, что, отклоняя эту гипотезу, мы или не ошибаемся (то есть гипотеза 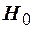 действительно ложная), или всё-таки совершаем ошибку первого рода, считая правильную гипотезу
действительно ложная), или всё-таки совершаем ошибку первого рода, считая правильную гипотезу 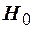 ложной. В последнем случае частота принятия ошибочного решения равна в среднем 5 из 100 случаев применения данного статистического критерия.
ложной. В последнем случае частота принятия ошибочного решения равна в среднем 5 из 100 случаев применения данного статистического критерия.
О. 3. Ошибкой второго рода называется ошибка принятия ложной гипотезы 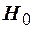 .
.
Вероятность совершения ошибки второго рода принято обозначать 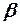 .
.
О. 4. Мощностью М критерия К называется вероятность 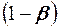 несовершения ошибки второго рода (мощность критерия К - это вероятность отклонения неверной гипотезы
несовершения ошибки второго рода (мощность критерия К - это вероятность отклонения неверной гипотезы 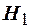 ).
).
51. Проверка гипотезы о равенстве математических
ожиданий двух нормальных генеральных
совокупностей при известной дисперсии
Проверка гипотез о равенстве двух центров распределения имеет важное практическое значение. Действительно, иногда оказывается, что средний результат одной серии экспериментов заметно отличается от среднего результата другой серии. При этом возникает вопрос: можно ли объяснить обнаруженное расхождение средних случайными ошибками экспериментов или оно вызвано какими-либо незамеченными или даже неизвестными закономерностями.
Сформулируем задачу сравнения двух центров распределения в общем виде. Рассмотрим две случайные величины 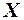 и
и  , каждая из которых подчиняется нормальному закону распределения. Пусть имеются две независимые выборки объёмами
, каждая из которых подчиняется нормальному закону распределения. Пусть имеются две независимые выборки объёмами  и
и  из генеральных совокупностей
из генеральных совокупностей 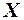 и
и  . Необходимо проверить гипотезу
. Необходимо проверить гипотезу 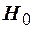 , заключающуюся в том, что
, заключающуюся в том, что  , относительно альтернативной гипотезы
, относительно альтернативной гипотезы 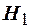 , состоящей в том, что
, состоящей в том, что  .
.
Так как в рассматриваемом случае дисперсии генеральных совокупностей 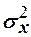 и
и  известны, а о значениях математических ожиданий
известны, а о значениях математических ожиданий 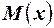 и
и  ничего неизвестно, то для проверки гипотезы
ничего неизвестно, то для проверки гипотезы 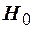 используем их оценки
используем их оценки 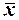 и
и 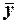 . Как известно, выборочные средние
. Как известно, выборочные средние 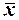 и
и 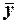 имеют нормальный закон распределения с параметрами
имеют нормальный закон распределения с параметрами 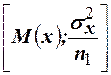 и
и 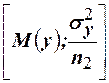 . Выборки независимы, поэтому
. Выборки независимы, поэтому 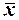 и
и 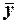 также независимы и случайная величина, равная разности между
также независимы и случайная величина, равная разности между 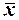 и
и 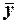 , имеет нормальное распределение, причём
, имеет нормальное распределение, причём  . Если гипотеза
. Если гипотеза 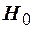 справедлива, то
справедлива, то 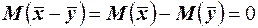 , следовательно, нормированная разность
, следовательно, нормированная разность 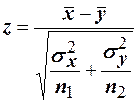 подчиняется нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Выбирая вероятность
подчиняется нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Выбирая вероятность  из соотношения
из соотношения  находим статистику
находим статистику  , которая разделит множество
, которая разделит множество  на два непересекающихся подмножества: область допустимых значений и критическую область. Те значения
на два непересекающихся подмножества: область допустимых значений и критическую область. Те значения  , при которых
, при которых 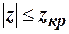 , образуют область допустимых значений; значения
, образуют область допустимых значений; значения  , для которых
, для которых  , определяют критическую область. Иными словами, если
, определяют критическую область. Иными словами, если 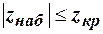 - нет оснований отвергнуть нулевую гипотезу или при заданном уровне значимости можно считать, что
- нет оснований отвергнуть нулевую гипотезу или при заданном уровне значимости можно считать, что  , если
, если 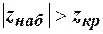 - то нулевую гипотезу отвергаем в пользу конкурирующей или при заданном уровне значимости можно считать что математические ожидания генеральных совокупностей различны.
- то нулевую гипотезу отвергаем в пользу конкурирующей или при заданном уровне значимости можно считать что математические ожидания генеральных совокупностей различны.
52. Сравнение выборочных средних при неизвестной
дисперсии генеральной совокупности.
Рассмотрим две случайные величины 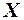 и
и  , каждая из которых подчиняется нормальному закону распределения с математическими ожиданиями
, каждая из которых подчиняется нормальному закону распределения с математическими ожиданиями 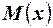 и
и 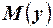 . Условимся считать, что
. Условимся считать, что 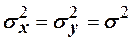 , числовое значение
, числовое значение  неизвестно. Пусть имеются две независимые выборки объёмами
неизвестно. Пусть имеются две независимые выборки объёмами  и
и  из генеральных совокупностей
из генеральных совокупностей 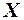 и
и  . Необходимо проверить гипотезу
. Необходимо проверить гипотезу 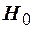 , заключающуюся в том, что
, заключающуюся в том, что 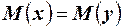 , относительно альтернативной гипотезы
, относительно альтернативной гипотезы 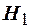 , состоящей в том, что
, состоящей в том, что 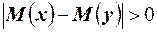 . Для оценки
. Для оценки 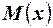 и
и 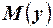 используем их оценки
используем их оценки 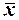 и
и 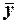 , а для оценки
, а для оценки  выборочные оценки:
выборочные оценки:  и
и 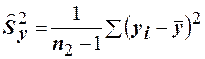 .
.
Так как генеральные совокупности 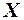 и
и  имеют одинаковые дисперсии, то для оценки
имеют одинаковые дисперсии, то для оценки  целесообразно использовать результаты обеих выборок. В математической статистике доказано, что лучшей оценкой для
целесообразно использовать результаты обеих выборок. В математической статистике доказано, что лучшей оценкой для  в данном случае является
в данном случае является 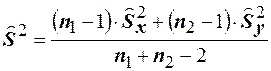 . В качестве выборочной оценки
. В качестве выборочной оценки  обычно принимают оценку
обычно принимают оценку  . Известно, что если случайная величина
. Известно, что если случайная величина 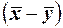 подчиняется нормальному закону, то статистика
подчиняется нормальному закону, то статистика
 имеет
имеет  - распределения Стьюдента с
- распределения Стьюдента с 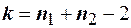 степенями свободы. Если гипотеза
степенями свободы. Если гипотеза 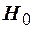 справедлива, то статистику t можно записать в виде:
справедлива, то статистику t можно записать в виде: 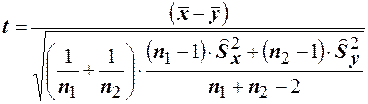 . Выбрав вероятность
. Выбрав вероятность 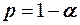 , по таблице
, по таблице  -распределения можно определить критическое значение
-распределения можно определить критическое значение 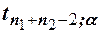 , для которого
, для которого  . Если вычисленное значение
. Если вычисленное значение 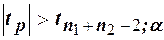 , то с надёжностью
, то с надёжностью 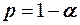 можно считать расхождение средних значимым (неслучайным).
можно считать расхождение средних значимым (неслучайным).
Пример 46. В результате двух серий измерений с количеством измерений 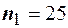 и
и  получены следующие выборочные средние
получены следующие выборочные средние 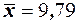 и
и 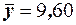 а также исправленные дисперсии
а также исправленные дисперсии  . Можно ли с надёжностью
. Можно ли с надёжностью 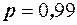 объяснить случайными причинами?
объяснить случайными причинами?
Решение. Вычислим исправленную дисперсию 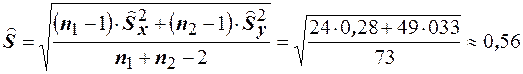 , вычисляем наблюдаемое значение статистики
, вычисляем наблюдаемое значение статистики  . Вероятности
. Вероятности 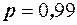 и числу степей свободы
и числу степей свободы  в таблице t – распределения (см. приложение табл.3) соответствует
в таблице t – распределения (см. приложение табл.3) соответствует 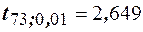 . Так как 1,38<2,649, то с надежностью 0,99 нельзя считать расхождение средних значимым, или при уровне значимости 0,99, можно считать, что математические ожидания
. Так как 1,38<2,649, то с надежностью 0,99 нельзя считать расхождение средних значимым, или при уровне значимости 0,99, можно считать, что математические ожидания 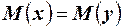 .
.
53.Сравнение выборочных дисперсий
Гипотезы о дисперсиях имеют особенно большое значение в технике, так как измеряемая дисперсией величина рассеяния характеризует такие важные показатели, как точность машин, приборов, технологических процессов.
Сформулируем гипотезу о равенстве дисперсий двух нормально распределенных генеральных совокупностей. Рассмотрим две случайные величины 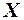 и
и  , каждая из которых подчиняется нормальному закону распределения с дисперсиями
, каждая из которых подчиняется нормальному закону распределения с дисперсиями 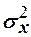 и
и 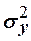 . Пусть из генеральных совокупностей
. Пусть из генеральных совокупностей 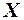 и
и  извлечены две независимые выборки объёмами
извлечены две независимые выборки объёмами  и
и 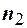 . Проверим гипотезу
. Проверим гипотезу 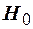 о том, что
о том, что  относительно альтернативной гипотезы
относительно альтернативной гипотезы 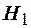 , заключающейся в том, что
, заключающейся в том, что  . Для оценки
. Для оценки 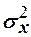 используем исправленную выборочную дисперсию
используем исправленную выборочную дисперсию 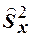 , а для оценки
, а для оценки  - исправленную выборочную дисперсию
- исправленную выборочную дисперсию 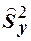 , следовательно, задача проверки гипотезы
, следовательно, задача проверки гипотезы 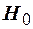 сводится к сравнению дисперсий
сводится к сравнению дисперсий 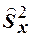 и
и 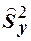 . Как показано ранее, случайные величины
. Как показано ранее, случайные величины  и
и 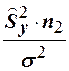 распределены по закону
распределены по закону 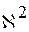 с
с  и
и 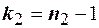 степенями свободы. Случайную величину
степенями свободы. Случайную величину 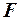 , определяемую соотношением
, определяемую соотношением 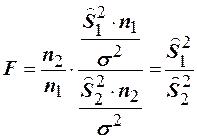 , называют случайной величиной с распределением Фишера-Снедекора. Заметим, что всегда можно так ввести обозначения, что
, называют случайной величиной с распределением Фишера-Снедекора. Заметим, что всегда можно так ввести обозначения, что 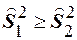 , поэтому случайная величина
, поэтому случайная величина 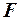 принимает значения, не меньшие единицы. Дифференциальный закон распределения случайной величины
принимает значения, не меньшие единицы. Дифференциальный закон распределения случайной величины 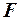 не содержит неизвестных параметров
не содержит неизвестных параметров 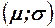 и их оценок, а зависит лишь от числа наблюдений в выборках
и их оценок, а зависит лишь от числа наблюдений в выборках  и
и 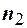 . Этот факт позволяет составить таблицы распределения случайной величины
. Этот факт позволяет составить таблицы распределения случайной величины 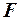 , в которых различным значениям уровня значимости и различным сочетаниям величин
, в которых различным значениям уровня значимости и различным сочетаниям величин 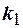 и
и  ставят в соответствие такие значения
ставят в соответствие такие значения 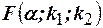 , для которых справедливо равенство
, для которых справедливо равенство  .
.
Сформулируем правило вычислив исправленные выборочные дисперсии 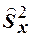 и
и 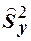 , найдём их отношение
, найдём их отношение 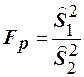 , причём в числителе запишем большую из них. Затем, выбрав необходимый уровень значимости
, причём в числителе запишем большую из них. Затем, выбрав необходимый уровень значимости 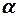 , по таблице
, по таблице 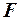 -распределения находим число
-распределения находим число 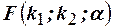 , которое сравниваем с вычисленным
, которое сравниваем с вычисленным 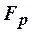 . Если окажется, что
. Если окажется, что  , то проверяемая гипотеза отвергается (различие между дисперсиями значимо), если
, то проверяемая гипотеза отвергается (различие между дисперсиями значимо), если 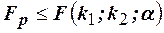 , то выборочные наблюдения не противоречат проверяемой гипотезе.
, то выборочные наблюдения не противоречат проверяемой гипотезе.
Пример 47. На двух станках обрабатываются детали. Отобраны две пробы: на первом станке 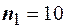 , на втором станке
, на втором станке  . По данным этих выборок рассчитаны исправленные выборочные дисперсии
. По данным этих выборок рассчитаны исправленные выборочные дисперсии  (для первого станка) и
(для первого станка) и 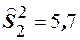 . Проверить при уровне значимости
. Проверить при уровне значимости  гипотезу о том, что станки обладают одинаковой точностью, или гипотезу
гипотезу о том, что станки обладают одинаковой точностью, или гипотезу 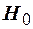 : дисперсии равны.
: дисперсии равны.
Решение. Вычислим значение 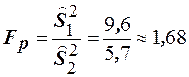 . Затем по уровню значимости
. Затем по уровню значимости  и степеням свободы
и степеням свободы  по таблице (см. приложение табл. 6) находим число
по таблице (см. приложение табл. 6) находим число 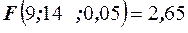 . Итак имеем 1,68<2,65, следовательно, предположение о равенстве дисперсий не противоречит наблюдениям, иными словами, нет оснований считать, что станки обладают разной точностью.
. Итак имеем 1,68<2,65, следовательно, предположение о равенстве дисперсий не противоречит наблюдениям, иными словами, нет оснований считать, что станки обладают разной точностью.
54. Проверка гипотез о законе распределения
Критерий согласия 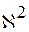 (Пирсона)
(Пирсона)
До сих пор мы рассматривали гипотезы, относящиеся к отдельным параметрам распределения случайной величины, причём закон распределения предполагался известным. Однако во многих практических задачах закон распределения случайной величины неизвестен, то есть является гипотезой, которая требует статистической проверки.
Обозначим через 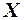 исследуемую случайную величину. Пусть требуется проверить гипотезу
исследуемую случайную величину. Пусть требуется проверить гипотезу 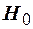 о том, что случайная величина подчиняется закону распределения
о том, что случайная величина подчиняется закону распределения  . Для проверки гипотезы произведём выборку, состоящую из п независимых наблюдений над случайной величиной
. Для проверки гипотезы произведём выборку, состоящую из п независимых наблюдений над случайной величиной 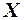 . По выборке можно построить эмпирическое распределение
. По выборке можно построить эмпирическое распределение 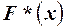 исследуемой случайной величины. Сравнение эмпирического
исследуемой случайной величины. Сравнение эмпирического 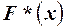 и теоретического распределений производится с помощью специально подобранной случайной величины - критерия согласия. Существует несколько критериев согласия:
и теоретического распределений производится с помощью специально подобранной случайной величины - критерия согласия. Существует несколько критериев согласия: 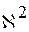 Пирсона, Колмогорова, Смирнова и др. Критерий согласия Пирсона - наиболее часто употребляемый критерий для проверки гипотезы о законе распределения.
Пирсона, Колмогорова, Смирнова и др. Критерий согласия Пирсона - наиболее часто употребляемый критерий для проверки гипотезы о законе распределения.
Рассмотрим этот критерий. Разобьём всю область изменения 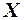 на
на 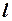 интервалов
интервалов 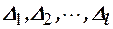 и подсчитаем количество элементов
и подсчитаем количество элементов  , попавших в каждый из интервалов
, попавших в каждый из интервалов 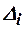 . Предполагая известным теоретический закон распределения
. Предполагая известным теоретический закон распределения  , всегда можно определить
, всегда можно определить 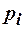 (вероятность попадания случайной величины
(вероятность попадания случайной величины 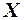 в интервал
в интервал 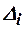 ), тогда теоретические частоты можно рассчитать по формуле
), тогда теоретические частоты можно рассчитать по формуле  . Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу
. Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу 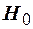 следует отвергнуть, в противном случае - принять.
следует отвергнуть, в противном случае - принять.
Сформулируем критерий, который бы характеризовал степень расхождения между эмпирическими и теоретическими частотами. В литературе по математической статистике доказывается, что статистика  имеет распределение
имеет распределение 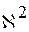 с
с 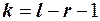 степенями свободы. Здесь
степенями свободы. Здесь 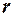 - число параметров распределения
- число параметров распределения  . Правило применения критерия
. Правило применения критерия 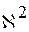 сводится к следующему. Рассчитав теоретические частоты
сводится к следующему. Рассчитав теоретические частоты  и вычислив значение
и вычислив значение  , затем выбрав уровень значимости критерия
, затем выбрав уровень значимости критерия 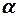 , по таблице находим
, по таблице находим 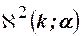 . Если
. Если 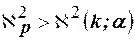 , то гипотезу
, то гипотезу 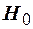 отвергают, если
отвергают, если 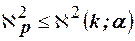 , то гипотезу принимают или, другими словами нет оснований отвергнуть гипотезу о том, что генеральная совокупность подчинена закону распределения
, то гипотезу принимают или, другими словами нет оснований отвергнуть гипотезу о том, что генеральная совокупность подчинена закону распределения  . В заключение отметим, что необходимым условием применения критерия Пирсона является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений. Если количество наблюдений мало, то нужно объединить интервалы, содержащие частоты менее 5.
. В заключение отметим, что необходимым условием применения критерия Пирсона является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений. Если количество наблюдений мало, то нужно объединить интервалы, содержащие частоты менее 5.
Пример 48. На телефонной станции производились наблюдения над числом 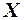 неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; 4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5. Определить выборочную среднюю и дисперсию неправильных соединений в минуту и проверить выполнение основного условия для распределения Пуассона
неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; 4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5. Определить выборочную среднюю и дисперсию неправильных соединений в минуту и проверить выполнение основного условия для распределения Пуассона 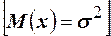 . Найти теоретическое распределение Пуассона и проверить степень согласия теоретического и эмпирического распределений по критерию
. Найти теоретическое распределение Пуассона и проверить степень согласия теоретического и эмпирического распределений по критерию 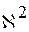 Пирсона при уровне значимости
Пирсона при уровне значимости  .
.
Решение. Упорядочим результаты наблюдений, записав их в таблицу:
Найдём 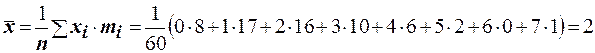 . Вычислим выборочную дисперсию по формуле
. Вычислим выборочную дисперсию по формуле 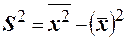 , где
, где 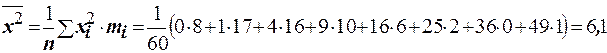 , тогда
, тогда  . Необходимое условие для распределения Пуассона практически выполняется. Запишем теоретический закон распределения Пуассона, используя вместо математического ожидания его оценку
. Необходимое условие для распределения Пуассона практически выполняется. Запишем теоретический закон распределения Пуассона, используя вместо математического ожидания его оценку 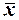 :
:  . Найдём теоретические частоты:
. Найдём теоретические частоты:
 ;
;
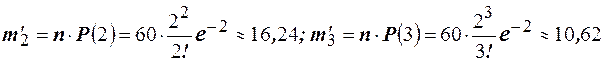 ;
;
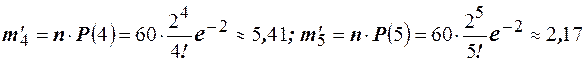 ;
;
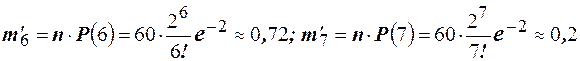 .
.
Так как последних три интервала содержат частоты менее пяти, то объединим их с предыдущим. Получим

|
|
|
|
|
|
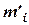
| 8,1
| 16,2
| 16,2
| 10,6
| 8,5
|
Вычислим значение 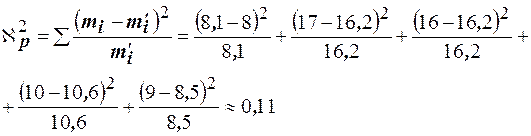
Примем уровень значимости 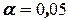 . Количество интервалов после объединения
. Количество интервалов после объединения  . По выборке вычислен один параметр, которым определяется закон Пирсона - математическое ожидание, следовательно:
. По выборке вычислен один параметр, которым определяется закон Пирсона - математическое ожидание, следовательно: 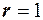 . Поэтому число степеней свободы
. Поэтому число степеней свободы  . По таблице (см. приложение табл.4) находим
. По таблице (см. приложение табл.4) находим 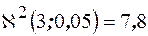 . Имеем 7,8>0,11, следовательно, нет оснований отвергнуть нулевую гипотезу или, другими словами, при уровне значимости
. Имеем 7,8>0,11, следовательно, нет оснований отвергнуть нулевую гипотезу или, другими словами, при уровне значимости  можно считать, что генеральная совокупность распределена по закону Пуассона.
можно считать, что генеральная совокупность распределена по закону Пуассона.
Пример 49. Проверить гипотезу о нормальном распределении для следующего интервального ряда:
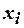
| 10-14
| 14-18
| 18-22
| 22-26
| 26-30
| 30-34
|

|
|
|
|
|
|
|
Решение. Найдём выборочное среднее по формуле 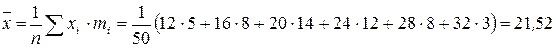
и исправленную дисперсию по формуле  , где
, где 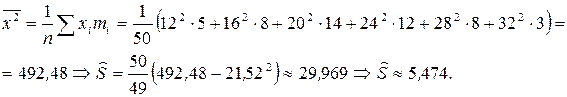
Найдем теоретические частоты по формуле 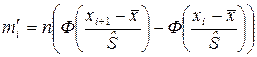 , тогда
, тогда 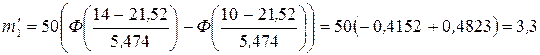
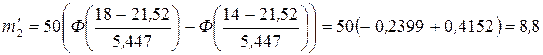
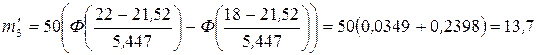
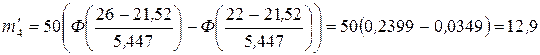
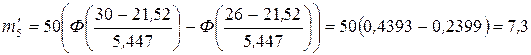
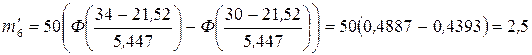
Так как последний и первый интервалы содержат частоты менее пяти, то объединим их с соседними. Получим

|
|
|
|
|
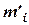
| 12,1
| 13,7
| 12,9
| 9,8
|
Найдём  по формуле
по формуле 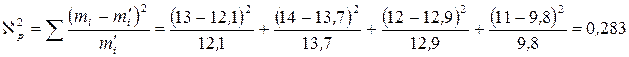 .
.
Число степеней свободы равно 4-3=1, следовательно, при уровне значимости  имеем по таблице
имеем по таблице  . Так как наблюдаемое значение меньше критического то гипотезу о нормальном распределении генеральной совокупности при заданном уровне значимости нет оснований отвергнуть.
. Так как наблюдаемое значение меньше критического то гипотезу о нормальном распределении генеральной совокупности при заданном уровне значимости нет оснований отвергнуть.
55. Выборочный коэффициент корреляции и его свойства
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из них ничтожно, а число их велико. В этом случае связь теряет свою однозначность, и изучаемая физическая система переходит не в определенное состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о статистической связи. Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение случайной переменной в предположении, что независимая переменная примет определённое значение.
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. Основная задача корреляционного анализа - выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости коэффициентов корреляции. Корреляционный анализ позволяет оценить функцию регрессии одной случайной величины на другую. Предпосылки корреляционного анализа следующие: 1) переменные величины должны быть случайными; 2) случайные величины должны иметь нормальное распределение.
Выборочный коэффициент корреляции находится по формуле
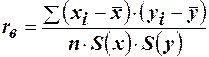
Выборочный коэффициент корреляции оценивает тесноту линейной связи.
Свойства выборочного коэффициента корреляции:
1. Коэффициент корреляции принимает значения на интервале  .
.
Доказательство. Докажем справедливость утверждения для дискретных переменных. Запишем явно неотрицательное выражение 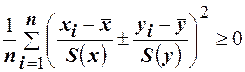 . Возведём выражение под знаком суммы в квадрат
. Возведём выражение под знаком суммы в квадрат  . Первое и третье слагаемые равны единице по определению дисперсии. Таким образом:
. Первое и третье слагаемые равны единице по определению дисперсии. Таким образом:  , откуда
, откуда  .
.
2. Выборочный коэффициент корреляции не зависит от выбора начала точки отсчёта и единицы измерения, то есть для любых 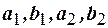 выполнено равенство
выполнено равенство
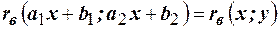 .
.
3. Выборочный коэффициент можно вычислять по формуле 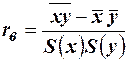 .
.

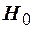 .
. совершения ошибки первого рода.
совершения ошибки первого рода. означает, что, отклоняя эту гипотезу, мы или не ошибаемся (то есть гипотеза
означает, что, отклоняя эту гипотезу, мы или не ошибаемся (то есть гипотеза 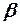 .
.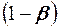 несовершения ошибки второго рода (мощность критерия К - это вероятность отклонения неверной гипотезы
несовершения ошибки второго рода (мощность критерия К - это вероятность отклонения неверной гипотезы 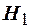 ).
).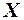 и
и  , каждая из которых подчиняется нормальному закону распределения. Пусть имеются две независимые выборки объёмами
, каждая из которых подчиняется нормальному закону распределения. Пусть имеются две независимые выборки объёмами  и
и  из генеральных совокупностей
из генеральных совокупностей  , относительно альтернативной гипотезы
, относительно альтернативной гипотезы  .
.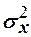 и
и  известны, а о значениях математических ожиданий
известны, а о значениях математических ожиданий 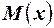 и
и  ничего неизвестно, то для проверки гипотезы
ничего неизвестно, то для проверки гипотезы 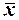 и
и 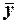 . Как известно, выборочные средние
. Как известно, выборочные средние 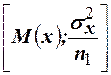 и
и 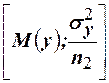 . Выборки независимы, поэтому
. Выборки независимы, поэтому  . Если гипотеза
. Если гипотеза 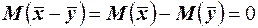 , следовательно, нормированная разность
, следовательно, нормированная разность 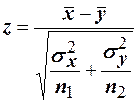 подчиняется нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Выбирая вероятность
подчиняется нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Выбирая вероятность  из соотношения
из соотношения  находим статистику
находим статистику  , которая разделит множество
, которая разделит множество  на два непересекающихся подмножества: область допустимых значений и критическую область. Те значения
на два непересекающихся подмножества: область допустимых значений и критическую область. Те значения 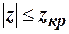 , образуют область допустимых значений; значения
, образуют область допустимых значений; значения  , определяют критическую область. Иными словами, если
, определяют критическую область. Иными словами, если 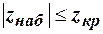 - нет оснований отвергнуть нулевую гипотезу или при заданном уровне значимости можно считать, что
- нет оснований отвергнуть нулевую гипотезу или при заданном уровне значимости можно считать, что 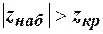 - то нулевую гипотезу отвергаем в пользу конкурирующей или при заданном уровне значимости можно считать что математические ожидания генеральных совокупностей различны.
- то нулевую гипотезу отвергаем в пользу конкурирующей или при заданном уровне значимости можно считать что математические ожидания генеральных совокупностей различны.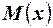 и
и 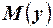 . Условимся считать, что
. Условимся считать, что 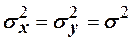 , числовое значение
, числовое значение  неизвестно. Пусть имеются две независимые выборки объёмами
неизвестно. Пусть имеются две независимые выборки объёмами 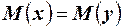 , относительно альтернативной гипотезы
, относительно альтернативной гипотезы 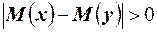 . Для оценки
. Для оценки  и
и 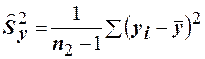 .
.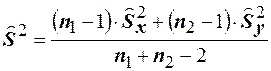 . В качестве выборочной оценки
. В качестве выборочной оценки  обычно принимают оценку
обычно принимают оценку  . Известно, что если случайная величина
. Известно, что если случайная величина 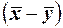 подчиняется нормальному закону, то статистика
подчиняется нормальному закону, то статистика имеет
имеет  - распределения Стьюдента с
- распределения Стьюдента с 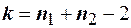 степенями свободы. Если гипотеза
степенями свободы. Если гипотеза 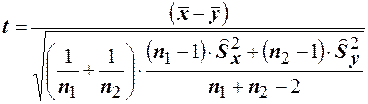 . Выбрав вероятность
. Выбрав вероятность 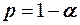 , по таблице
, по таблице 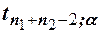 , для которого
, для которого  . Если вычисленное значение
. Если вычисленное значение 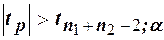 , то с надёжностью
, то с надёжностью 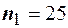 и
и  получены следующие выборочные средние
получены следующие выборочные средние 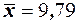 и
и 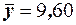 а также исправленные дисперсии
а также исправленные дисперсии  . Можно ли с надёжностью
. Можно ли с надёжностью 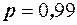 объяснить случайными причинами?
объяснить случайными причинами?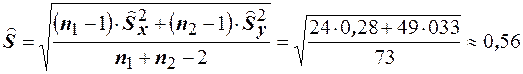 , вычисляем наблюдаемое значение статистики
, вычисляем наблюдаемое значение статистики  . Вероятности
. Вероятности  в таблице t – распределения (см. приложение табл.3) соответствует
в таблице t – распределения (см. приложение табл.3) соответствует 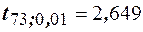 . Так как 1,38<2,649, то с надежностью 0,99 нельзя считать расхождение средних значимым, или при уровне значимости 0,99, можно считать, что математические ожидания
. Так как 1,38<2,649, то с надежностью 0,99 нельзя считать расхождение средних значимым, или при уровне значимости 0,99, можно считать, что математические ожидания 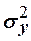 . Пусть из генеральных совокупностей
. Пусть из генеральных совокупностей  и
и 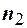 . Проверим гипотезу
. Проверим гипотезу 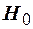 о том, что
о том, что  относительно альтернативной гипотезы
относительно альтернативной гипотезы 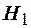 , заключающейся в том, что
, заключающейся в том, что  . Для оценки
. Для оценки 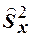 , а для оценки
, а для оценки 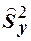 , следовательно, задача проверки гипотезы
, следовательно, задача проверки гипотезы  и
и 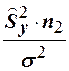 распределены по закону
распределены по закону 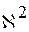 с
с  и
и 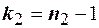 степенями свободы. Случайную величину
степенями свободы. Случайную величину 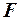 , определяемую соотношением
, определяемую соотношением 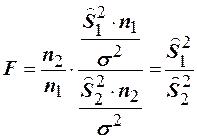 , называют случайной величиной с распределением Фишера-Снедекора. Заметим, что всегда можно так ввести обозначения, что
, называют случайной величиной с распределением Фишера-Снедекора. Заметим, что всегда можно так ввести обозначения, что 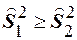 , поэтому случайная величина
, поэтому случайная величина 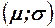 и их оценок, а зависит лишь от числа наблюдений в выборках
и их оценок, а зависит лишь от числа наблюдений в выборках 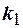 и
и  ставят в соответствие такие значения
ставят в соответствие такие значения 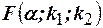 , для которых справедливо равенство
, для которых справедливо равенство  .
.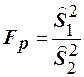 , причём в числителе запишем большую из них. Затем, выбрав необходимый уровень значимости
, причём в числителе запишем большую из них. Затем, выбрав необходимый уровень значимости 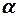 , по таблице
, по таблице 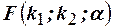 , которое сравниваем с вычисленным
, которое сравниваем с вычисленным 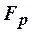 . Если окажется, что
. Если окажется, что  , то проверяемая гипотеза отвергается (различие между дисперсиями значимо), если
, то проверяемая гипотеза отвергается (различие между дисперсиями значимо), если 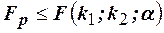 , то выборочные наблюдения не противоречат проверяемой гипотезе.
, то выборочные наблюдения не противоречат проверяемой гипотезе.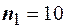 , на втором станке
, на втором станке  . По данным этих выборок рассчитаны исправленные выборочные дисперсии
. По данным этих выборок рассчитаны исправленные выборочные дисперсии  (для первого станка) и
(для первого станка) и 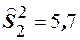 . Проверить при уровне значимости
. Проверить при уровне значимости  гипотезу о том, что станки обладают одинаковой точностью, или гипотезу
гипотезу о том, что станки обладают одинаковой точностью, или гипотезу 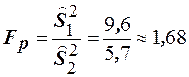 . Затем по уровню значимости
. Затем по уровню значимости  по таблице (см. приложение табл. 6) находим число
по таблице (см. приложение табл. 6) находим число 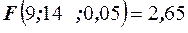 . Итак имеем 1,68<2,65, следовательно, предположение о равенстве дисперсий не противоречит наблюдениям, иными словами, нет оснований считать, что станки обладают разной точностью.
. Итак имеем 1,68<2,65, следовательно, предположение о равенстве дисперсий не противоречит наблюдениям, иными словами, нет оснований считать, что станки обладают разной точностью.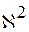 (Пирсона)
(Пирсона)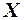 исследуемую случайную величину. Пусть требуется проверить гипотезу
исследуемую случайную величину. Пусть требуется проверить гипотезу  . Для проверки гипотезы произведём выборку, состоящую из п независимых наблюдений над случайной величиной
. Для проверки гипотезы произведём выборку, состоящую из п независимых наблюдений над случайной величиной 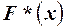 исследуемой случайной величины. Сравнение эмпирического
исследуемой случайной величины. Сравнение эмпирического 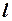 интервалов
интервалов 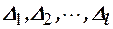 и подсчитаем количество элементов
и подсчитаем количество элементов  , попавших в каждый из интервалов
, попавших в каждый из интервалов 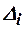 . Предполагая известным теоретический закон распределения
. Предполагая известным теоретический закон распределения 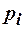 (вероятность попадания случайной величины
(вероятность попадания случайной величины  . Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу
. Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу  имеет распределение
имеет распределение 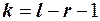 степенями свободы. Здесь
степенями свободы. Здесь 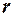 - число параметров распределения
- число параметров распределения  , затем выбрав уровень значимости критерия
, затем выбрав уровень значимости критерия 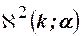 . Если
. Если 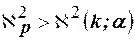 , то гипотезу
, то гипотезу 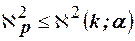 , то гипотезу принимают или, другими словами нет оснований отвергнуть гипотезу о том, что генеральная совокупность подчинена закону распределения
, то гипотезу принимают или, другими словами нет оснований отвергнуть гипотезу о том, что генеральная совокупность подчинена закону распределения 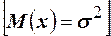 . Найти теоретическое распределение Пуассона и проверить степень согласия теоретического и эмпирического распределений по критерию
. Найти теоретическое распределение Пуассона и проверить степень согласия теоретического и эмпирического распределений по критерию 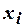

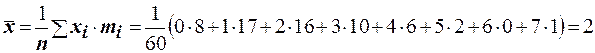 . Вычислим выборочную дисперсию по формуле
. Вычислим выборочную дисперсию по формуле 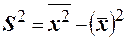 , где
, где 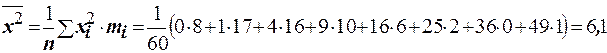 , тогда
, тогда  . Необходимое условие для распределения Пуассона практически выполняется. Запишем теоретический закон распределения Пуассона, используя вместо математического ожидания его оценку
. Необходимое условие для распределения Пуассона практически выполняется. Запишем теоретический закон распределения Пуассона, используя вместо математического ожидания его оценку 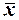 :
:  . Найдём теоретические частоты:
. Найдём теоретические частоты: ;
;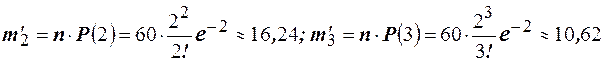 ;
;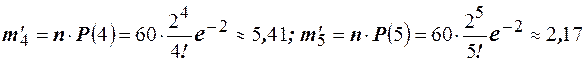 ;
;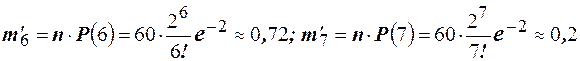 .
.
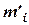
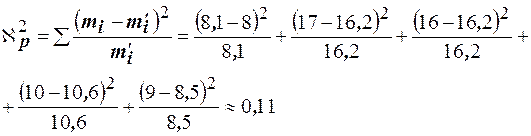
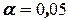 . Количество интервалов после объединения
. Количество интервалов после объединения  . По выборке вычислен один параметр, которым определяется закон Пирсона - математическое ожидание, следовательно:
. По выборке вычислен один параметр, которым определяется закон Пирсона - математическое ожидание, следовательно: 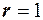 . Поэтому число степеней свободы
. Поэтому число степеней свободы  . По таблице (см. приложение табл.4) находим
. По таблице (см. приложение табл.4) находим 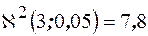 . Имеем 7,8>0,11, следовательно, нет оснований отвергнуть нулевую гипотезу или, другими словами, при уровне значимости
. Имеем 7,8>0,11, следовательно, нет оснований отвергнуть нулевую гипотезу или, другими словами, при уровне значимости 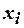
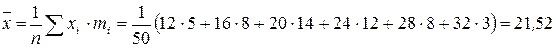
 , где
, где 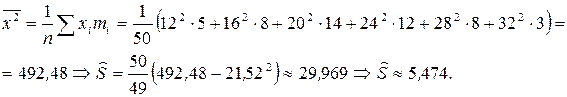
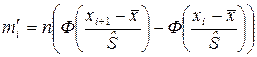 , тогда
, тогда 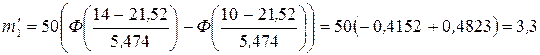
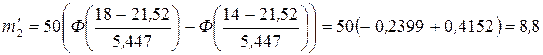
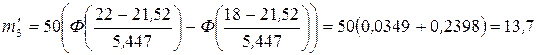
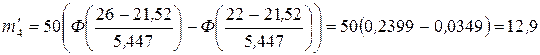
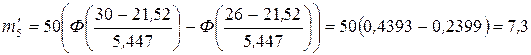
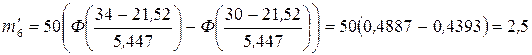
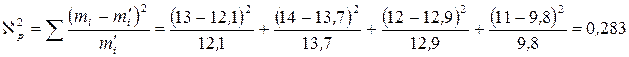 .
. . Так как наблюдаемое значение меньше критического то гипотезу о нормальном распределении генеральной совокупности при заданном уровне значимости нет оснований отвергнуть.
. Так как наблюдаемое значение меньше критического то гипотезу о нормальном распределении генеральной совокупности при заданном уровне значимости нет оснований отвергнуть.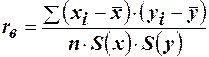
 .
.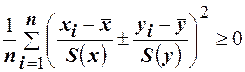 . Возведём выражение под знаком суммы в квадрат
. Возведём выражение под знаком суммы в квадрат  . Первое и третье слагаемые равны единице по определению дисперсии. Таким образом:
. Первое и третье слагаемые равны единице по определению дисперсии. Таким образом:  , откуда
, откуда  .
.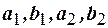 выполнено равенство
выполнено равенство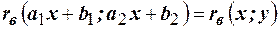 .
.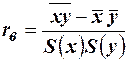 .
.


