Критические точки распределения Стьюдента
| Число степеней свободы k
| Уровень значимости 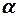 (двусторонняя критическая область) (двусторонняя критическая область)
| | 0.10
| 0.05
| 0.02
| 0.01
| 0.002
| 0.001
| |
| 6,31
| 12,7
| 31,82
| 63,7
| 318,3
| 637,0
| |
| 2,92
| 4,30
| 6,97
| 9,92
| 22,33
| 31,6
| |
| 2,35
| 3,18
| 4,54
| 5,84
| 10,22
| 12,9
| |
| 2,13
| 2,78
| 3,75
| 4,60
| 7,17
| 8,61
| |
| 2,01
| 2,57
| 3,37
| 4,03
| 5,89
| 6,86
| |
| 1,94
| 2,45
| 3,14
| 3,71
| 5,21
| 5,96
| |
| 1,89
| 2,36
| 3,00
| 3,50
| 4,79
| 5,40
| |
| 1,86
| 2,31
| 2,90
| 3,36
| 4,50
| 5,04
| |
| 1,83
| 2,26
| 2,82
| 3,25
| 4,30
| 4,78
| |
| 1,81
| 2,23
| 2,76
| 3,17
| 4,14
| 4,59
| |
| 1,80
| 2,20
| 2,72
| 3,11
| 4,03
| 4,44
| |
| 1,78
| 2,18
| 2,68
| 3,05
| 3,93
| 4,32
| |
| 1,77
| 2,16
| 2,65
| 3,01
| 3,85
| 4,22
| |
| 1,76
| 2,14
| 2,62
| 2,98
| 3,79
| 4,14
| |
| 1,75
| 2,13
| 2,60
| 2,95
| 3,73
| 4,07
| |
| 1,75
| 2,12
| 2,58
| 2,92
| 3,69
| 4,01
| |
| 1,74
| 2,11
| 2,57
| 2,90
| 3,65
| 3,96
| |
| 1,73
| 2,10
| 2,55
| 2,88
| 3,61
| 3,92
| |
| 1,73
| 2,09
| 2,54
| 2,86
| 3,55
| 3,85
| |
| 1,73
| 2,09
| 2,53
| 2,85
| 3,55
| 3,85
| |
| 1,70
| 2,04
| 2,46
| 2,75
| 3,39
| 3,65
| |
| 1,68
| 2,02
| 2,42
| 2,70
| 3,31
| 3,55
| |
| 1,67
| 2,00
| 2,39
| 2,66
| 3,23
| 3,46
| 
| 1,64
| 1,96
| 2,33
| 2,58
| 3,09
| 3,29
| | Число степеней свободы k
| 0.05
| 0.025
| 0.01
| 0.005
| 0.001
| 0.0005
| Уровень значимости 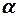 (односторонняя критическая область) (односторонняя критическая область)
|
Таблица 6
Критические точки распределения F Фишера-Снедекора
(k 1 – число степеней свободы большей дисперсии,
k 2 – число степеней свободы меньшей дисперсии)
Уровень значимости 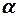 =0,01 =0,01
| | k 1
k 2
|
|
|
|
|
|
|
|
|
|
| |
| 29,46
| 28,71
| 28,24
| 27,91
| 27,67
| 27,49
| 27,34
| 27,23
| 27,13
| 27,05
| |
| 16,69
| 15,98
| 15,52
| 15,21
| 14,98
| 14,80
| 14,66
| 14,54
| 14,45
| 14,37
| |
| 12,06
| 11,39
| 10,97
| 10,67
| 10,45
| 10,27
| 10,15
| 10,05
| 9,96
| 9,89
| |
| 9,78
| 9,15
| 8,75
| 8,47
| 8,26
| 8,10
| 7,98
| 7,87
| 7,79
| 7,72
| |
| 8,45
| 7,85
| 7,46
| 7,19
| 7,00
| 6,84
| 6,71
| 6,62
| 6,54
| 6,47
| |
| 7,59
| 7,01
| 6,63
| 6,37
| 6,19
| 6,03
| 5,91
| 5,82
| 5,74
| 5,67
| |
| 6,99
| 6,42
| 6,06
| 5,80
| 5,62
| 5,47
| 5,35
| 5,26
| 5,18
| 5,11
| |
| 6,55
| 5,99
| 5,64
| 5,39
| 5,21
| 5,06
| 4,95
| 4,85
| 4,78
| 4,71
| |
| 6,22
| 5,67
| 5,32
| 5,07
| 4,88
| 4,74
| 4,63
| 4,54
| 4,46
| 4,40
| |
| 5,95
| 5,41
| 5,06
| 4,82
| 4,65
| 4,50
| 4,39
| 4,30
| 4,22
| 4,16
| |
| 5,74
| 5,20
| 4,86
| 4,62
| 4,44
| 4,30
| 4,19
| 4,10
| 4,02
| 3,96
| |
| 5,56
| 5,03
| 4,69
| 4,46
| 4,28
| 4,14
| 4,03
| 3,94
| 3,86
| 3,80
| |
| 5,42
| 4,89
| 4,56
| 4,32
| 4,14
| 4,00
| 3,89
| 3,80
| 3,73
| 3,67
| |
| 5,29
| 4,77
| 4,44
| 4,20
| 4,03
| 3,89
| 3,78
| 3,69
| 3,61
| 3,55
| Уровень значимости 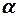 =0,05 =0,05
| |
| 9,28
| 9,12
| 9,01
| 8,94
| 8,88
| 8,84
| 8,81
| 8,78
| 8,76
| 8,74
| |
| 6,59
| 6,39
| 6,26
| 6,16
| 6,09
| 6,04
| 6,00
| 5,96
| 5,93
| 5,91
| |
| 5,41
| 5,19
| 5,05
| 4,95
| 4,88
| 4,82
| 4,78
| 4,74
| 4,70
| 4,68
| |
| 4,76
| 4,53
| 4,39
| 4,28
| 4,21
| 4,15
| 4,10
| 4,06
| 4,03
| 4,00
| |
| 4,35
| 4,12
| 3,97
| 3,87
| 3,79
| 3,73
| 3,68
| 3,63
| 3,60
| 3,57
| |
| 4,07
| 3,84
| 3,69
| 3,58
| 3,50
| 3,44
| 3,39
| 3,34
| 3,31
| 3,28
| |
| 3,86
| 3,63
| 3,48
| 3,37
| 3,29
| 3,23
| 3,18
| 3,13
| 3,10
| 3,07
| |
| 3,71
| 3,48
| 3,33
| 3,22
| 3,14
| 3,07
| 3,02
| 2,97
| 2,94
| 2,94
| |
| 3,59
| 3,36
| 3,20
| 3,09
| 3,01
| 2,95
| 2,90
| 2,86
| 2,82
| 2,79
| |
| 3,49
| 3,26
| 3,11
| 3,00
| 2,92
| 2,85
| 2,80
| 2,76
| 2,72
| 2,69
| |
| 3,41
| 3,18
| 3,02
| 2,92
| 2,84
| 2,77
| 2,72
| 2,67
| 2,63
| 2,60
| |
| 3,34
| 3,11
| 2,96
| 2,85
| 2,77
| 2,70
| 2,65
| 2,60
| 2,56
| 2,53
| |
| 3,29
| 3,06
| 2,90
| 2,79
| 2,70
| 2,64
| 2,59
| 2,55
| 2,51
| 2,48
| |
| 3,24
| 3,01
| 2,85
| 2,74
| 2,66
| 2,59
| 2,54
| 2,49
| 2,45
| 2,42
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Дезинфекция предметов ухода, инструментов однократного и многократного использования
Дезинфекция изделий медицинского назначения проводится с целью уничтожения патогенных и условно-патогенных микроорганизмов - вирусов (в т...
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
|
Предпосылки, условия и движущие силы психического развития Предпосылки –это факторы. Факторы психического развития –это ведущие детерминанты развития чел. К ним относят: среду...
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
|
|