Показатели вариации
Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, то есть вариацию. Простейшим показателем вариации является вариационный размах Вариационный размах – приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты которые используются для его вычисления, как правило, ненадёжны. Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической. Средним линейным отклонением Эмпирической дисперсией Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднее квадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака. Для вариационного ряда среднее квадратическое отклонение:
|
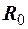, равный разности между наибольшим и наименьшим вариантами: 
.
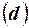называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней арифметической 
.
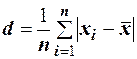называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней арифметической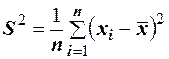 
. Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия 
.
.
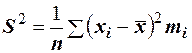