Случайные события
1. Элементы комбинаторики Факториал. Функция Пример 1. Перестановки. Каждая последовательность Пример 2. Сколькими способами можно расставить шесть книг на полке? Решение. Число способов равно числу перестановок из шести элементов, то есть Размещение. Любой упорядочный набор k различных элементов множества М, содержащего n элементов, называется размещением k элементов из n. Число размещений обозначается символом Пример 3. Сколькими способами можно распределить три первых места для восьми участвующих в соревновании команд? Решение. Так как нас интересует, какая из команд займёт первое, второе и третье места, то есть порядок среди отобранных трёх команд, используем размещение. Тогда число способов найдём по формуле Сочетание. Любое подмножество из k различных элементов множества М, содержащего n элементов, называется сочетанием. Число сочетаний обозначается символом Пример 4. Найти число способов отобрать три цветка из семи. Решение. Так как порядок среди цветов нам не важен, то используем сочетание. Число способов найдём по формуле
2. Алгебра событий О. 1. Событие называется случайным, если в результате опыта оно может либо произойти, либо не произойти. О. 2. Событие называется достоверным, если оно обязательно происходит в результате опыта. О. 3. Событие называется невозможным, если оно не может произойти в данном опыте. О. 4. События называются несовместными, если они не могут произойти в одном опыте. О. 5. Событие А благоприятствует событию В, если из появления события А следует, что произошло событие В. О. 6. События образуют полную группу, если в результате опыта произойдёт хотя бы одно из них. О. 7. Событие С называется суммой событий А В, если оно состоит в появлении события А или появлениисобытия В. Сумма событий обозначается О. 8. Событие С называется произведением событий А В, если оно состоит в появлении события А и появлении события В. Обозначается О. 9. Событие С называется разностью событий А В, если оно состоит в появлении события А и не появлении события В. Обозначается О. 10. Событие О. 11. События называются равновозможными, если нет объективных оснований считать, одно более возможным чем другое. О. 12. Равновозможные, несовместные образующие полную группу события называются исходами данного опыта. 3. Классическое определение вероятности О. 1. Вероятностью событияназывается численная мера степени объективной возможности появления этого события. О. 2. (Классическое определение вероятности) Вероятностью события А называется отношение числа благоприятствующих исходов к общему числу исходов данного опыта. Вероятность события А обозначается Основные свойства вероятности 1. Вероятность достоверного события равна единице. 2. Вероятность невозможного события равна нулю. 3. Для любого события А его вероятность заключена в интервале 4. Вероятность наступления противоположного события Пример 5. Из урны, содержащей 12 чёрных и 8 белых шаров, наудачу вынуто два шара. Найти вероятность того, что они разного цвета. Решение. Обозначим событие А – шары разного цвета, тогда по определению Пример 6. Из колоды карт наудачу вынуто две. Найти вероятность того, что они обе бубновой масти. Колода содержит 36 карт. Решение. По классическому определению вероятности имеем Тогда
|

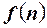 , определенная на множестве целых, неотрицательных чисел, для которой
, определенная на множестве целых, неотрицательных чисел, для которой 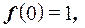
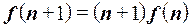 , называется n -факториалом и обозначается
, называется n -факториалом и обозначается  . Для любого натурального n имеем
. Для любого натурального n имеем 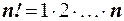 .
.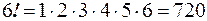 .
. различных элементов с учётом их порядка называется перестановкой этих элементов. Число перестановок обозначается
различных элементов с учётом их порядка называется перестановкой этих элементов. Число перестановок обозначается  и находится по формуле
и находится по формуле 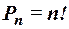 .
.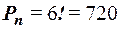 .
. и находится по формуле
и находится по формуле 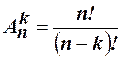 .
.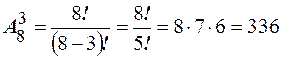 .
. и находится по формуле
и находится по формуле  .
. .
.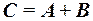 .
. .
.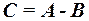 .
. называется противоположным событию А, если оно состоит в не появлении события А.
называется противоположным событию А, если оно состоит в не появлении события А.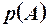 . Тогда
. Тогда  , где
, где 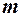 - число благоприятных для появления события А исходов,
- число благоприятных для появления события А исходов,  .
.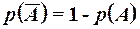 .
.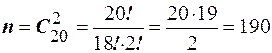 . Число благоприятных исходов равно числу способов отобрать один шар из 8 и один шар из 12, так как союз и, то общее число благоприятных исходов равно произведению
. Число благоприятных исходов равно числу способов отобрать один шар из 8 и один шар из 12, так как союз и, то общее число благоприятных исходов равно произведению 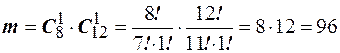 . Поэтому искомая вероятность равна
. Поэтому искомая вероятность равна  .
.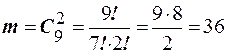 ,
, 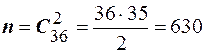 .
.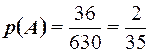 .
.


