Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.
О. 1. Медианой  называют значение признака, приходящее на середину ранжированного ряда наблюдений.
называют значение признака, приходящее на середину ранжированного ряда наблюдений.
Пусть проведено нечётное число наблюдений, то есть 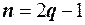 , и результаты наблюдений проранжированы и выписаны в следующий ряд
, и результаты наблюдений проранжированы и выписаны в следующий ряд 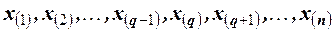 . Здесь
. Здесь 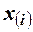 - значение признака, занявшее i -е порядковое место в ранжированом ряду. На середину ряда приходится значение
- значение признака, занявшее i -е порядковое место в ранжированом ряду. На середину ряда приходится значение  . Следовательно:
. Следовательно: 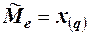 .
.
Если проведено чётное число наблюдений, то есть  , то на середину ранжированного ряда
, то на середину ранжированного ряда  приходятся значения
приходятся значения  и
и  . В этом случае за медиану принимают среднюю арифметическую значений
. В этом случае за медиану принимают среднюю арифметическую значений  и
и  , то есть
, то есть 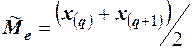 .
.
Для интервального вариационного ряда медиана определяется по формуле 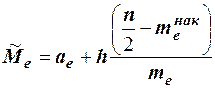 или
или  , где
, где  - начало медианного интервала, то есть такого, которому соответствует первая из накопленных частот (накопленных частостей), большая или равная половине всех наблюдений
- начало медианного интервала, то есть такого, которому соответствует первая из накопленных частот (накопленных частостей), большая или равная половине всех наблюдений  ;
; 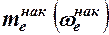 - частота (частость), накопленная к началу медианного интервала;
- частота (частость), накопленная к началу медианного интервала;  - частота (частость) медианного интервала.
- частота (частость) медианного интервала.
О. 2. Модой  называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ей является вариант, которому соответствует наибольшая частота.
называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ей является вариант, которому соответствует наибольшая частота.
В случае интервального вариационного ряда мода вычисляется по следующей формуле:
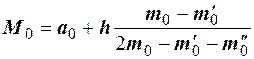 или
или  ,
,
где  - начало модального интервала, то есть такого, которому соответствует наибольшая частота (частость);
- начало модального интервала, то есть такого, которому соответствует наибольшая частота (частость);  - частота (частость) модального интервала;
- частота (частость) модального интервала;  - частота (частость) интервала, предшествующего модальному;
- частота (частость) интервала, предшествующего модальному; 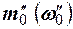 - частота (частость) интервала, следующего за модальным.
- частота (частость) интервала, следующего за модальным.
Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости. Модальные производительность и себестоимость помогают вскрыть ресурсы, имеющиеся в экономике.
Пример 37. Вычислить моду и медиану для интервального ряда
| Интервалы
| 3 - 7
| 7 - 11
| 11 - 15
| 15 - 19
| 19 - 23
| 23 – 27
|
| Частоты
|
|
|
|
|
|
|
Решение. Найдём объём выборки по формуле  , или
, или 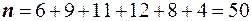 . Вычислим накопленные частоты
. Вычислим накопленные частоты
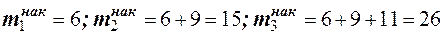 , следовательно, медианным является интервал
, следовательно, медианным является интервал  . Тогда
. Тогда  ,
, 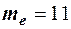 и
и 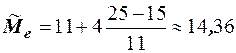 .
.
Модальным является интервал 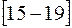 , следовательно,
, следовательно, 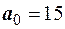 ,
, 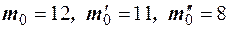 . Тогда
. Тогда  .
.

 называют значение признака, приходящее на середину ранжированного ряда наблюдений.
называют значение признака, приходящее на середину ранжированного ряда наблюдений.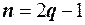 , и результаты наблюдений проранжированы и выписаны в следующий ряд
, и результаты наблюдений проранжированы и выписаны в следующий ряд 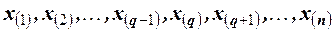 . Здесь
. Здесь 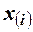 - значение признака, занявшее i -е порядковое место в ранжированом ряду. На середину ряда приходится значение
- значение признака, занявшее i -е порядковое место в ранжированом ряду. На середину ряда приходится значение  . Следовательно:
. Следовательно: 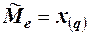 .
. , то на середину ранжированного ряда
, то на середину ранжированного ряда  приходятся значения
приходятся значения  . В этом случае за медиану принимают среднюю арифметическую значений
. В этом случае за медиану принимают среднюю арифметическую значений 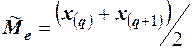 .
.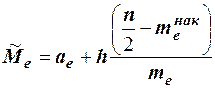 или
или  , где
, где  - начало медианного интервала, то есть такого, которому соответствует первая из накопленных частот (накопленных частостей), большая или равная половине всех наблюдений
- начало медианного интервала, то есть такого, которому соответствует первая из накопленных частот (накопленных частостей), большая или равная половине всех наблюдений  ;
; 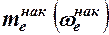 - частота (частость), накопленная к началу медианного интервала;
- частота (частость), накопленная к началу медианного интервала;  - частота (частость) медианного интервала.
- частота (частость) медианного интервала. называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ей является вариант, которому соответствует наибольшая частота.
называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ей является вариант, которому соответствует наибольшая частота.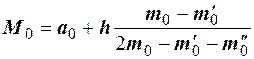 или
или  ,
, - начало модального интервала, то есть такого, которому соответствует наибольшая частота (частость);
- начало модального интервала, то есть такого, которому соответствует наибольшая частота (частость);  - частота (частость) модального интервала;
- частота (частость) модального интервала;  - частота (частость) интервала, предшествующего модальному;
- частота (частость) интервала, предшествующего модальному; 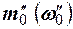 - частота (частость) интервала, следующего за модальным.
- частота (частость) интервала, следующего за модальным. , или
, или 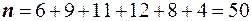 . Вычислим накопленные частоты
. Вычислим накопленные частоты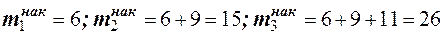 , следовательно, медианным является интервал
, следовательно, медианным является интервал  . Тогда
. Тогда  ,
, 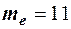 и
и 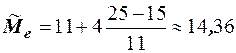 .
.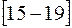 , следовательно,
, следовательно, 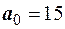 ,
, 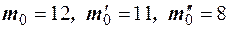 . Тогда
. Тогда  .
.


