| ТЕОРИЯ ВЕРОЯТНОСТЕЙ
|
|
| Случайные события
|
| 1. Элементы комбинаторики
|
|
| 2. Алгебра событий
|
|
| 3. Классическое определение вероятности
|
|
| 4. Геометрическая вероятность
|
|
| 5. Теоремы сложения
|
|
| 6. Теоремы умножения
|
|
| 7. Формула полной вероятности
|
|
| 8. Формула Байеса
|
|
| 9. Схема независимых испытаний.
Формула Бернулли
|
|
| 10. Наивероятнейшее число появления событий
|
|
| 11. Локальная теорема Муавра-Лапласа
|
|
| 12. Интегральная теорема Муавра-Лапласа
|
|
| 13. Формула Пуассона
|
|
| Случайные величины
|
|
| 14. Закон распределения случайной величины
|
|
| 15. Функция распределения
|
|
| 16. Плотность распределения
|
|
| 17. Математическое ожидание
|
|
| 18. Дисперсия и среднее квадратическое отклонение
|
|
| 19. Начальные и центральные моменты
|
|
| 20. Равномерное распределение
|
|
| 21. Нормальное распределение
|
|
| 22. Биномиальное распределение
|
|
| 23. Распределение Пуассона
Закон распределения редких явлений
|
|
| 24. Показательное распределение
|
|
| Закон больших чисел
|
|
| 25. Лемма Маркова
|
|
| 26. Неравенство Чебышева
|
|
| 27. Теорема Чебышева
|
|
| МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
|
|
| 28. Основные понятия математической статистики
|
|
| 29. Вариационные ряды
|
|
| 30. Графическое изображение вариационного ряда
|
|
| 31. Эмпирическая функция распределения
|
|
| 32. Средние величины
|
|
| 33. Медиана и мода
|
|
| 34. Показатели вариации
|
|
| 35. Эмпирические центральные начальные и моменты
|
|
| 36. Эмпирические асимметрия и эксцесс
|
|
| 37. Метод условных вариантов для расчёта основных числовых характеристик вариационного ряда
|
|
| 38. Статистическое оценивание параметров распределения
|
|
| 39. Основные свойства оценок
|
|
| 40. Оценка математического ожидания и дисперсии
|
|
| 41. Метод максимального правдоподобия
|
|
| 42. Метод наименьших квадратов
|
|
| 43. Распределение средней арифметической для выборок из нормальной генеральной совокупности. Распределение Стьюдента
|
|
44. Распределение дисперсии в выборках из нормальной генеральной совокупности. Распределение 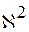 Пирсона Пирсона
|
|
| 45. Понятие доверительного интервала. Доверительная вероятность
|
|
| 46. Доверительный интервал для математического ожидания при известной дисперсии генеральной совокупности
|
|
| 47. Доверительный интервал для математического ожидания при неизвестной дисперсии генеральной совокупности
|
|
| 48. Доверительный интервал для дисперсии
|
|
| 49. Понятие статистической гипотезы. Общая постановка за дачи проверки гипотез
|
|
| 50. Ошибки, допускаемые при проверке статистических гипотез Уровень значимости статистического критерия
|
|
| 51. Проверка гипотезы о равенстве математических ожиданий двух нормальных генеральных совокупностей при известной дисперсии.
|
|
| 52. Сравнение выборочных средних при неизвестной дисперсии генеральной совокупности
|
|
| 53. Сравнение выборочных дисперсий
|
|
54. Проверка гипотез о законе распределения. Критерий согласия 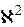 (Пирсона) (Пирсона)
|
|
| 55. Выборочный коэффициент корреляции и его свойства
|
|
| 56. Метод вычисления выборочного коэффициента корреляции для вариационных рядов
|
|
| 57. Проверка гипотезы о значимости коэффициента корреляции
|
|
| 58. Эмпирическая и теоретическая линии регрессии
|
|
| 59. Значимость коэффициентов регрессии
|
|
| 59. Корреляционное отношение
|
|
| Приложение
|
|