4 страница. Из определения следует, что
Где Из определения следует, что т.е. ковариация СВ с самой собой есть ее дисперсия. Для дискретных случайных величин: Для непрерывных случайных величин: Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяни е вокруг точки 1. Ковариация двух независимых случайных величин равна нулю. 2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е. 3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е. Ковариация, как уже отмечено, характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она - величина размерная, ее размерность определяется произведением размерностей случайных величин. Это затрудняет использование ковариации для оценки степени зависимости для различных случайных величин. Этих недостатков лишен коэффициент корреляции. Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:
Из определения следует, что Свойства коэффициента корреляции: 1. Коэффициент корреляции принимает значения на отрезке [-1;1], т.е. 2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю. Т.о., из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость. 3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость. 26. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии. Определение. Случайная величина (Х,Y) называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:
Где Из определения следует, что двумерный нормальный закон распределения определяется пятью параметрами:
Т.о., параметры Нетрудно убедиться в том, что каждый из условных законов распределения случайных величин Х и Y является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:
Теорема. Если две нормально распределенные случайные величины Х и Y некоррелированы, то они независимы. Т.о., для нормально распределенных случайных величин термины «некоррелированность» и «независимость» равносильны. 27. Неравенство Маркова (лемма Чебышева) (с выводом). Пример. Теорема. Если СВ Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство:
☺ Доказательство проведем для дискретной СВ Х. Расположим ее значения в порядке возрастания, из которых часть значений
Запишем выражение для математического ожидания М(Х): где Отбрасывая первые k неотрицательных слагаемых (напомним, что все Заменяя в неравенстве значения Cумма вероятностей в левой части полученного неравенства представляет собой сумму вероятностей событий Т.к. события Х > А и Х ≤ А противоположные, то заменяя Р(Х > А) выражением 1 - Р(Х ≤ А), придем к другой форме неравенства Маркова:
Неравенство Маркова применимо к любым неотрицательным случайным величинам. Пример. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500. Решение. а) По условию М(Х) = 300. По формуле б) По формуле 28. Неравенство Чебышева (с выводом) и его частные случаидля случайной величины, распределенной по биномиальному закону, и для частости события. Теорема. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева: где а = М(Х), е > 0. ☺ Применим неравенство Маркова в форме Т.к. неравенство Учитывая, что события Неравенство Чебышева применимо для любых случайных величин. В форме Запишем неравенство Чебышева в форме а) для СВ Х = m, имеющей биноминальный закон распределения с математическим ожиданием а = М(Х) = nр и дисперсией D(X) = npq: б) для частости 3амечание. Если М(Х) > А или Это означает, что применение указанных неравенств в этих случаях приведет к тривиальному результату: вероятность события больше отрицательного числа либо меньше числа, превосходящего 1. 30. Теорема Чебышева (с доказательством), ее значение и следствие. Пример. Теорема. Если дисперсии n независимых случайных величин
Или
☺ По условию Получим неравенство Чебышева в форме Найдем математическое ожидание М(Х) и оценку дисперсии D(Х):
(Здесь использованы свойства математического ожидания и дисперсии и, в частности, то, что случайные величины Запишем неравенство
Т.к. по доказанному Следовательно в пределе при n → ∞ величина Подчеркнем смысл теоремы Чебышева. При большом числе n случайных величин практически достоверно, что их средняя величина случайная, как угодно мало отличается от неслучайной величины, т.е. практически перестает быть случайной. Следствие. Если независимые случайные величины
Или
Теорема Чебышева и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь; при этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту/убытки страхователя при наступлении страхового случая как величину случайную и обладая известной статистикой таких случаев, можно определить среднее число/средние убытки при наступлении страховых случаев, которое на основании теоремы Чебышева с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса. Без учета действия закона больших чисел (теоремы Чебышева) возможны существенные убытки страховой компании (при занижении размера страхового взноса), либо потеря привлекательности страховых услуг (при завышении размера взноса). 31. Закон больших чисел. Теорема Бернулли (с доказательством) и ее значение. Пример. Под законам больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. Теорема. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:
Или ☺ Заключение теоремы непосредственно вытекает из неравенства Чебышева для частости события Смысл теоремы Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость (или статистическая вероятность) события m/n - величина случайная, как угодно мало отличается от неслучайной величины р - вероятности события, т.е. практически перестает быть случайной. Теорема Бернулли является следствием теоремы Чебышева. 32. Неравенство Чебышева для средней арифметической случайных величин (с выводом).
33. Центральная предельная теорема. Понятие о теореме Ляпунова и ее значение. Пример. Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при к-ых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова. Теорема Ляпунова. Если
то закон распределения суммы Например, потребление электроэнергии для бытовых нужд за месяц в каждой квартире многоквартирного дома можно представить в виде n различных случайных величин. Если потребление электроэнергии в каждой квартире по своему значению резко не выделяется среди остальных, то на основании теоремы Ляпунова можно считать, что потребление электроэнергии всего дома, т.е. сумма n независимых случайных величин будет случайной величиной, имеющей приближенно нормальный закон распределения. Если, например, в одном из помещений дома разместится вычислительный центр, у которого уровень потребления электроэнергии несравнимо выше, чем в каждой квартире для бытовых нужд, то вывод о приближенно нормальном распределении потребления электроэнергии всего дома будет неправомерен, так как нарушено условие (6.20), ибо потребление электроэнергии вычислительного центра будет играть превалирующую роль в образовании всей суммы потребления. Следствие. Если В частности, если все случайные величины 34. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощенный способ их расчета. Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами (частотами или частостями). При изучении вариационных рядов наряду с понятием частоты используется понятие накопленной частоты (обозначаем Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный. Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты (частости) или накопленные частоты (частости). Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и - непрерывным (интервальными), если варианты могут отличаться один от другого на сколь угодно малую величину. Для графического изображения вариационных рядов наиболее часто используются полигон, гистограмма, кумулятивная кривая: Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты ( Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака Кумулятивная кривая (кумулята) - кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломаную, соединяющую точки ( Эмпирической функцией pacпpeдeлeнuя
Другими словами, для данного х эмпирическая функция распределения представляет накопленную частость: Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величины Х). Вариационный ряд содержит достаточно полную информацию об изменчивости (вариации) признака. Однако обилие числовых данных, с помощью которых он задается, усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов: средних или характеристик центральной тенденции; характеристик изменчивости (вариации) и др. Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:
где Очевидно, что Основные свойства средней арифметической. 1. Средняя арифметическая постоянной равна самой постоянной. 2. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
3. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число:
4. Средняя арифметическая отклонений вариантов от средней арифметической равна нулю:
5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:
6. Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп:
где Дисперсией
Формулу для дисперсии вариационного ряда можно записать в виде: где Для несгруппированного ряда Дисперсию
|

 ,
,  .
.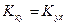 . Кроме того,
. Кроме того, 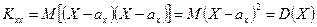 .
. .
. .
. . Об этом, в частности, свидетельствуют свойства ковариации случайных величин.
. Об этом, в частности, свидетельствуют свойства ковариации случайных величин. , или
, или  .
. .
. .
. . Очевидно также, что коэффициент корреляции есть безразмерная величина.
. Очевидно также, что коэффициент корреляции есть безразмерная величина. .
.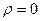 .
.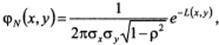
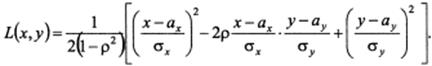
 .
.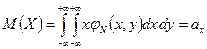 и аналогично
и аналогично  .;
.; и аналогично
и аналогично 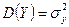 .;
.;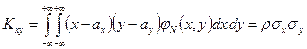 .
. и
и 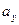 выражают математические ожидания случайных величин Х и Y, параметры
выражают математические ожидания случайных величин Х и Y, параметры  и
и 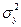 - их дисперсии, а
- их дисперсии, а  - коэффициент корреляции между случайными величинами Х и Y.
- коэффициент корреляции между случайными величинами Х и Y.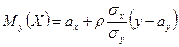 ,
, 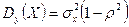 ,
, ,
,  .
.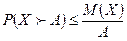
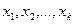 будут не более числа А, а другая часть -
будут не более числа А, а другая часть -  будут больше А, т.е.
будут больше А, т.е.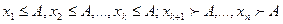 (рис. 6.1).
(рис. 6.1).
 ,
, - вероятности того, что СВ Х примет значения соответственно
- вероятности того, что СВ Х примет значения соответственно 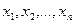 .
. ), получим:
), получим:  .
. или
или 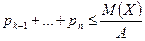 .
. , т.е. вероятность события Х>А. Поэтому
, т.е. вероятность события Х>А. Поэтому  .☻
.☻ .
. т.е. вероятность того, что число вызовов превысит 400, будет не более 0,75.
т.е. вероятность того, что число вызовов превысит 400, будет не более 0,75. т.е. вероятность того, что число вызовов не более 500, будет не менее 0,4.
т.е. вероятность того, что число вызовов не более 500, будет не менее 0,4.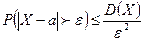 ,
,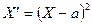 , взяв в качестве положительного числа
, взяв в качестве положительного числа  . Получим:
. Получим:  .
.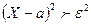 равносильно неравенству
равносильно неравенству 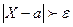 , а
, а 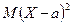 есть дисперсия случайной величины Х, то из неравенства получаем доказываемое неравенство. ☻
есть дисперсия случайной величины Х, то из неравенства получаем доказываемое неравенство. ☻ противоположны, неравенство Чебышева можно записать и в другой форме:
противоположны, неравенство Чебышева можно записать и в другой форме:  .
. оно устанавливает верхнюю границу, а в форме
оно устанавливает верхнюю границу, а в форме  .
. события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью
события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 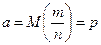 и имеющей дисперсию
и имеющей дисперсию  :
: 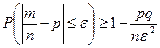 .
.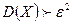 , то правые части неравенств Маркова и Чебышева в форме соответственно
, то правые части неравенств Маркова и Чебышева в форме соответственно 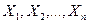 ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий
ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий  , т.е.
, т.е.
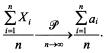
 ,
, 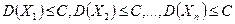 , где С - постоянное число.
, где С - постоянное число. .
.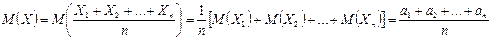 ;
;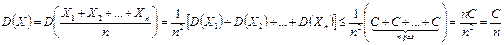 .
.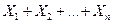 независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)
независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)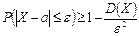 для случайной величины
для случайной величины  :
: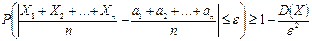 .
.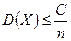 , то
, то  ,
, .
.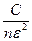 стремится к нулю, и получим доказываемую формулу. ☻
стремится к нулю, и получим доказываемую формулу. ☻ ,
,



 независимые случайные величины, у каждой из которых существует матем-кое ожидание
независимые случайные величины, у каждой из которых существует матем-кое ожидание  , дисперсия
, дисперсия  , абсолютный центральный момент третьего порядка
, абсолютный центральный момент третьего порядка  и
и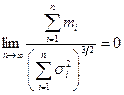 (6.20)
(6.20) при n → ∞ неограниченно приближается к нормальному с матем-ким ожиданием
при n → ∞ неограниченно приближается к нормальному с матем-ким ожиданием 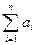 и дисперсией
и дисперсией  .
.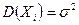 и абсолютные центральные моменты третьего порядка
и абсолютные центральные моменты третьего порядка  одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.
одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.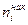 ). Накопленная частота показывает, ск-ко наблюдалось вариантов со значением признака, меньшим х. Отношение на копленной частоты к общему числу наблюдений n назовем накопленной частостью
). Накопленная частота показывает, ск-ко наблюдалось вариантов со значением признака, меньшим х. Отношение на копленной частоты к общему числу наблюдений n назовем накопленной частостью  .
.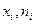 ), i = 1, 2,..., m.
), i = 1, 2,..., m. , i = 1, 2,..., m, и высотами, равными частотам (частостям)
, i = 1, 2,..., m, и высотами, равными частотам (частостям)  (
( ) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.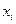 ,
, 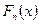 называется относительная частота (частость) того, что признак (случайная величина х) примет значение, меньшее заданного х, т.е.
называется относительная частота (частость) того, что признак (случайная величина х) примет значение, меньшее заданного х, т.е.
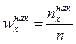 .
.
 .
. , где
, где  - частости вариантов или интервалов.
- частости вариантов или интервалов. .
.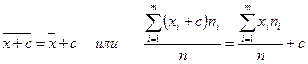 .
.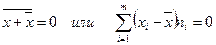 .
. .
.
 - общая средняя (средняя арифметическая всего ряда);
- общая средняя (средняя арифметическая всего ряда); 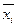 - групповая средняя i-й группы, объем которой равен
- групповая средняя i-й группы, объем которой равен  вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической: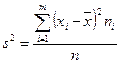 .
.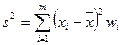
 :
:  .
.


