5 страница. Вычисление средней арифметической и дисперсии вариационного ряда можно упростить, если использовать не первоначальные варианты (i = 1
Вычисление средней арифметической
где с и k - специально подобранные постоянные. Согласно свойствам 2 и 3 средней арифметической и дисперсии:
Откуда
Затем, получим Теперь, заменяя в (4) и (5)
где Формулы (7) и (8) дадут заметное упрощение расчетов, если в качестве постоянной k взять величину (ширину) интервала по x, а в качестве с - середину серединного интервала. Если серединных интервалов два (при четном числе интервалов), то в качестве с рекомендуется взять середину одного из этих интервалов, например, имеющего большую частоту. Генеральная и выборочная совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода. Вся подлежащая изучению совокупность объектов (наблюдений) называется генеральной совокупностью. В матем-кой статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, к-ые могли бы быть произведены при данном реальном комплексе условий, и в этом смысле его не следует смешивать с реальными совокупностями, подлежащими статистическому изучению. Так, обследовав даже все пр-тия подотрасли по определенным технико-эк-ким показателям, мы можем рассматривать обследованную совокупность лишь как представителя гипотетически возможной более широкой совокупности пр-тий, к-е могли бы функционировать в рамках того же реального комплекса условий. Понятие генеральной совокупности в определенном смысле аналогично понятию случайной величины (закону распределения вер-тей, вероятностному пространству), т.к. полностью обусловлено определенным комплексом условий. Та часть объектов, к-ая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью, или выборкой. Числа объектов (наблюдений) в генеральной или выборочной совокупности называются их объёмами. Генеральная совокупность может иметь как конечный, так и бесконечный объем. Выборку можно рассматривать как некий эмпирический аналог генеральной совокупности. Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (по выборке) выносить суждение о ее свойствах в целом. Преимущества выборочного метода наблюдения по сравнению со сплошным: 1) позволяет существенно экономить затраты ресурсов (материальных, трудовых, временных); 2) является единственно возможным в случае бесконечной генеральной совокупности или в случае, когда исследование связано с уничтожением наблюдаемых объектов (напр, исследование долговечности электрических лампочек, предельных режимов работы приборов и т.п.); 3) при тех же затратах ресурсов дает возможность проведения углубленного исследования за счет расширения программы исследования; 4) позволяет снизить ошибки регистрации, т.е. расхождения между истинным и зарегистрированным значениями признака. Основной недостаток выборочною метода - ошибки исследования, называемые ошибками репрезентативности (представительства). Однако неизбежные ошибки, возникающие при выборочном методе исследования в связи с изучением только части объектов, могут быть заранее оценены и посредством правильной организации выборки сведены к практически незначимым величинам. Между тем использование сплошного наблюдения даже там, где это принципиально возможно, не говоря уже о росте трудоемкости, стоимости и увеличении необходимого времени, часто приводит к тому, что каждое отдельное наблюдение поневоле проводится с меньшей точностью. А это уже сопряжено с неустранимыми ошибками и в конечном счете может привести к снижению точности сплошного наблюдения по сравнению с выборочным. Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она д.б. отобрана случайно. Случайность отбора элементов в выборку достигается соблюдением принципа равной возможности всем элементам генеральной совокупности быть отобранными в выборку. На практике это достигается тем, что извлечение элементов в выборку проводится путем жеребьевки (лотереи) или с помощью случайных чисел, имеющихся в специальных таблицах или вырабатываемых ЭВМ с помощью датчика случайных чисел. Выборка называется репрезентативной (представительной), если она достаточно хорошо воспроизводит генеральную совокупность. Различают следующие виды выборок: 1) собственно-случайная выборка, образованная случайным выбором элементов без расчленения на части или группы; 2) механическая выборка, в к-ую элементы из генеральной совокупности отбираются через определенный интервал. На пример, если объем выборки должен составлять 10% (10%-ная выборка), то отбирается каждый l0-й ее элемент и т.д.; 3) типическая (стратифицированная) выборка, в к-ую случайным образом отбираются элементы из типических групп, на к-ые по нек-му признаку разбивается генеральная совокупность; 4) серийная (гнездовая) выборка, в к-ую случайным образом отбираются не элементы, а целые группы совокупности (серии), а сами серии подвергаются сплошному наблюдению. Используют два способа образования выборки: 1) повторный отбор (по схеме возвращенного шара), когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и м.б. повторно отобран; 2) бесповторный отбор (по схеме невозвращенного шара), когда отобранный элемент не возвращается в общую совокупность. Мат-кая теория выборочного метода основывается на анализе собственно-случайной выборки. Обозначим:
N и n - объемы генеральной и выборочной совокупностей;
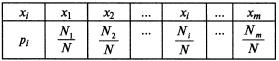
М и m - число элементов генеральной и выборочной совокупностей, обладающих данным признаком. Средние арифметические распределения признака в генеральной и выборочной совокупностях называются соответственно генеральной и выборочной средними, а дисперсии этих распределений - генеральной и выборочной дисперсиями. Отношение числа элементов генеральной и выборочной совокупностей, обладающих нек-ым признаком А, к их объемам, называются соответственно генеральной и выборочной долями. Все формулы сведем в таблицу.
Замечание. В случае бесконечной генеральной совокупности (N = ∞) под генеральными средней и дисперсией понимается соответственно математическое ожидание Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки. Теоретическую основу применимости выборочного метода составляет закон больших чисел, согласно к-му при неограниченном увеличении объема выборки практически достоверно, что случайные выборочные характеристики как угодно близко приближаются (сходятся по вероятности) к определенным параметрам генеральной совокупности. 36. Понятие об оценке параметров генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность. Сформулируем задачу оценки параметров в общем виде. Пусть распределение признака Х - генеральной совокупности - задается функцией вер-тей Для вычисления параметра Определение. Оценкой
Поскольку О качестве оценки следует судить не по индивидуальным ее значениям, а лишь по распределению ее значений в большой сети испытаний, т.е. по выборочному распределению оценки. Если значения оценки Свойства оценок. Определение. Оценка в противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка Если при конечном объеме выборки n Определение. Оценка
В случае использования состоятельных оценок оправдывается увеличение объема выборки, т.к. при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. Если оценка состоятельна, то практически достоверно, что при достаточно большом n Если оценка
Определение. Несмещенная оценка Т.к. для не смещенной оценки Эффективность оценки определяют отношением: где 37. Оценка генеральной доли по собственно-случайной выборке. Несмещенность и состоятельность выборочной доли. Пусть генеральная совок-ть содержит N элементов, из к-ых М обладает нек-ым признаком А. Следует найти «наилучшую» оценку генеральной доли а) Выборка повторная.
Случайные величины Теорема. Выборочная доля ☺ Докажем вначале несмещенность оценки w. Матем-кое ожидание и дисперсия частости события в n независимых испытаниях, в каждом из к-рых оно может наступить с одной и той же вероятностью р, равны соответственно
Т.к. вер-ть того, что любой отобранный в выборку элемент обладает признаком А, есть генеральная доля р, то из 1 равенства вытекает, что частость или выборочная доля w есть несмещенная оценка генеральной доли р. Осталось доказать состоятельность оценки б) Выборка бесповторная. В случае бесповторной выборки СВ Теорема. Выборочная доля
☺ Очевидно, что и для бесповторной выборки Найдем дисперсию выборочной доли для бесповторной выборки:
При выводе формулы использовали то, что СВ Х = m в случае бесповтoрной выборки имеет гипергеометрическое распределение, и ее дисперсия определяется по формуле 38. Оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней. Пусть из генеральной совокупности объема N отобрана случайная выборка Рассмотрим в качестве такой возможной оценки выборочнyю среднюю х, т.е. а) Выборка повторная. Закон распределения для каждой случайной величины
Найдем числовые характеристики СВ
т.е. мат-кое ожидание и дисперсия каждой СВ Теорема. Выборочная средняя □ Докажем вначале несмещенность оценки. Найдем мат-кое ожидание выборочной средней
Осталось доказать состоятельность оценки б) Выборка бесповторная В этом случае случайные величины Теорема. Выборочная средняя
39. Оценка генеральной дисперсии по собственно-случайной выборке. Смещенность и состоятельность выборочной дисперсии (без вывода). Исправленная выборочная дисперсия. На первый взгляд, наиболее подходящей оценкой для генеральной дисперсии Теорема. Выборочная дисперсия Δ Принимая без док-ва состоятельность оценки
Полагая а) Выборка повторная Для повторной выборки выборочные значения рассматриваем как независимые случайные величины Найдем мат-кое ожидание оценки
Первый член в правой части Второй член с учетом того, что Поэтому б) Выборка бесповторная Для бесповторной выборки
Итак, и для повторной выборки, и для бесповторной Т.к.
|

 и дисперсии
и дисперсии  вариационного ряда можно упростить, если использовать не первоначальные варианты
вариационного ряда можно упростить, если использовать не первоначальные варианты 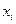 (i = 1, 2,..., m), а новые варианты:
(i = 1, 2,..., m), а новые варианты: , (1)
, (1)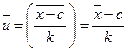 , (2)
, (2)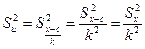 , (3)
, (3)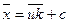 (4)
(4)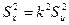 . (5)
. (5) (6)
(6) и
и 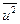 их выражениями
их выражениями  и
и  через варианты
через варианты 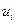 , получим
, получим , (7)
, (7) , (8)
, (8)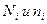 - число элементов генеральной и выборочной совокупностей со значением признака
- число элементов генеральной и выборочной совокупностей со значением признака 
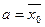 и дисперсия
и дисперсия  распределения признака Х (генеральной совокупности), а под генеральной долей р - вероятность данного события.
распределения признака Х (генеральной совокупности), а под генеральной долей р - вероятность данного события.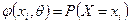 (для дискретной СВ Х) или плотностью вер-ти
(для дискретной СВ Х) или плотностью вер-ти 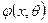 (для непрерывной СВ Х), к-ая содержит неизвестный параметр
(для непрерывной СВ Х), к-ая содержит неизвестный параметр 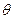 . Напр, это параметр λ в распределении Пуассона или параметры а и
. Напр, это параметр λ в распределении Пуассона или параметры а и 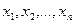 . Эти значения можно рассматривать как частные значения (реализации) n независимых случайных величин
. Эти значения можно рассматривать как частные значения (реализации) n независимых случайных величин  каждая из к-ых имеет тот же закон распределения, что и сама СВ Х.
каждая из к-ых имеет тот же закон распределения, что и сама СВ Х. параметра
параметра 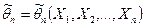 .
. , было по возможности меньшим. Таково основное условие, к-му должна удовлетворять «наилучшая» оценка.
, было по возможности меньшим. Таково основное условие, к-му должна удовлетворять «наилучшая» оценка. .
. , либо занижать его (если
, либо занижать его (если 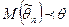 ). Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
). Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.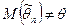 , т.е. смещение оценки
, т.е. смещение оценки  , но
, но  , то такая оценка
, то такая оценка  , или
, или 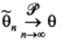 .
. .
.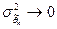 при n → ∞, то оценка
при n → ∞, то оценка 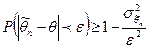 .
.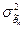 , то эф-ть является решающим свойством, определяющим качество оценки.
, то эф-ть является решающим свойством, определяющим качество оценки. .
. и
и 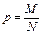 . Рассмотрим в качестве такой возможной оценки параметра р его статистический аналог - выборочную долю
. Рассмотрим в качестве такой возможной оценки параметра р его статистический аналог - выборочную долю  .
. Выборочную долю можно представить как среднюю арифметическую n альтернативных случайных величин
Выборочную долю можно представить как среднюю арифметическую n альтернативных случайных величин  , т.е.
, т.е.  , где каждая СВ
, где каждая СВ  (k=1,2,…,n) выражает число появлений признака в k-м элементе выборки (т.е. при наличии признака
(k=1,2,…,n) выражает число появлений признака в k-м элементе выборки (т.е. при наличии признака  , при его отсутствии
, при его отсутствии  ) и имеет один и тот же закон распределения:
) и имеет один и тот же закон распределения: , Где q = 1 – p.
, Где q = 1 – p.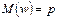 ,
, 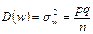 .
.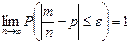 , или
, или  . ☻
. ☻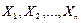 будут зависимыми.
будут зависимыми.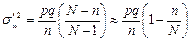 .
. ,
, .
. .
. Случайные величины
Случайные величины 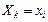 (k=1,2,...n; i=1,2,...,m) и их комбинации.
(k=1,2,...n; i=1,2,...,m) и их комбинации. , (1)
, (1) . (2)
. (2) повторной выборки есть несмещенная и состоятельная оценка генеральной средней
повторной выборки есть несмещенная и состоятельная оценка генеральной средней 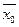 причем
причем 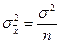 .
. .
. или
или 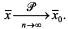
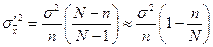 .
.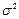 является выборочная дисперсия
является выборочная дисперсия 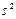 . Следующая теорема свидетельствует о том, что
. Следующая теорема свидетельствует о том, что 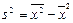 . На основании свойства 3 средней арифметической и дисперсии, если все значения признака уменьшить на одно и то же число С, то средняя уменьшится на это число, т.е.
. На основании свойства 3 средней арифметической и дисперсии, если все значения признака уменьшить на одно и то же число С, то средняя уменьшится на это число, т.е.  , а дисперсия не изменится:
, а дисперсия не изменится: .
. , получим
, получим  .
.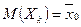 M,
M, 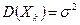 , k = 1,2,...,n.
, k = 1,2,...,n. .
. .
. ,
, 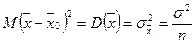 .
. .
. (т.к. объем генеральной совокупности N, как правило, большой и N ≈ N -1).
(т.к. объем генеральной совокупности N, как правило, большой и N ≈ N -1). , т.е
, т.е  и
и  , то выборочная дисперсия (в n среднем, полученная по разным выборкам) занижает генеральную дисперсию. Поэтому, заменяя
, то выборочная дисперсия (в n среднем, полученная по разным выборкам) занижает генеральную дисперсию. Поэтому, заменяя 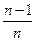 . Тогда с учетом (
. Тогда с учетом (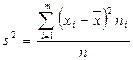 ) получим «исправленную» выборочную дисперсию:
) получим «исправленную» выборочную дисперсию:


