Параметры зубчатого колеса, получаемые при нарезании зубьев
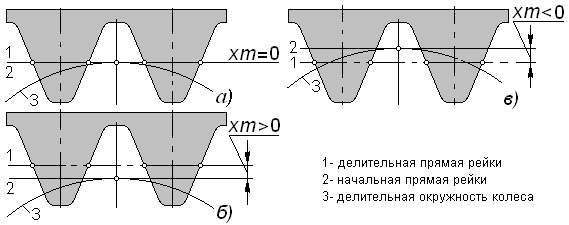
Коэффициент смещения. Взаимное положение колеса и заготовки при нарезании зубьев можно охарактеризовать положением делительной прямой инструментальной рейки относительно делительной окружности нарезаемого колеса (рис. 5.7); расстояние между ними называют смещением исходного контура, его выражают в количестве модулей, как xm.
Безразмерную величину x называют коэффициентом смещения; это алгебраическая величина и здесь различают три случая, показанные рис. 5.7, а – в. Нарезая зубья при различных коэффициентах смещения, можно целенаправленно влиять на размеры и форму этих зубьев, а также на свойства колес и составленных из них передач. Часть параметров и размеров зубчатого колеса не зависит от коэффициента смещения; к таковым относятся: модуль m; угол профиля эвольвенты на делительной окружности (равен углу профиля исходного контура) a; шаг по дуге основной окружности (основной шаг)
Значения этих трех параметров у нарезаемого колеса те же, что и у зуборезного инструмента. Также не зависят от x: диаметр делительной окружности (делительный диаметр)
диаметр основной окружности (основной диаметр)
При нарезании зубьев поверхность их вершин не формируется, т.е. диаметр окружности вершин колеса
На рис. 5.8 изображены профиль зуба реечного производящего контура (а) и формируемый им при нарезании профиль зуба колеса (б). Во время нарезания начальная прямая 2 производящей рейки перекатывается без скольжения по делительной окружности колеса. На указанных профилях отмечены соответствующие друг другу точки и участки профилей; в частности: - эвольвентный участок AL профиля нарезаемого зуба формируется прямолинейным участком - переходная кривая LF на профиле зуба колеса формируется круговой кромкой - вершина зуба рейки, параллельная ее делительной прямой 1, формирует окружность впадин диаметра Очевидно, что часть профиля зуба рейки, расположенная выше точки Найдем размеры колеса, зависящие от коэффициента смещения x:
|

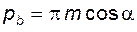 . (5.12)
. (5.12) ; (5.13)
; (5.13)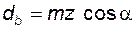 . (5.14)
. (5.14) (диаметр вершин) остается равным диаметру заготовки; следовательно, нарезание зубьев – это попросту удаление материала из впадин колеса.
(диаметр вершин) остается равным диаметру заготовки; следовательно, нарезание зубьев – это попросту удаление материала из впадин колеса.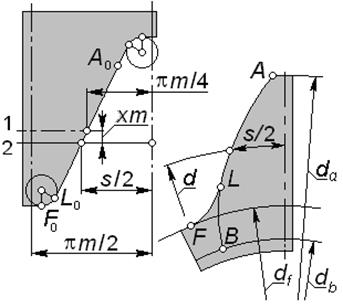
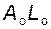 профиля зуба рейки;
профиля зуба рейки; профиля зуба рейки;
профиля зуба рейки; колеса.
колеса. , в профилировании нарезаемого зуба не участвует.
, в профилировании нарезаемого зуба не участвует.


