Тангенс угла профиля в нижней граничной точке эвольвенты
Согласно (5.5), диаметр окружности граничных точек
при
эвольвента в точке L плавно сопрягается с переходной кривой Величину Из (5.18) также видно, что у колеса, имеющего z зубьев и нарезанного с коэффициентом смещения x, подрезание отсутствует, если
Величину Подрезание ослабляет зуб у основания, укорачивает эвольвентный участок профиля и его обычно стараются избегать; условием отсутс–твия подрезания является соблюдение любого из неравенств:
Толщина зуба Угол профиля в точке Y, принадлежащей окружности диаметра
если эта точка принадлежит делительной окружности (т.е.
В таком случае из рис. 5.10 следует, что искомая толщина зуба равна
Формулу (5.23) используют, например, для нахождения толщины зуба
Окружность, на которой расположена точка пересечения двух разноименных эвольвент, ограничивающих профиль одного и того же зуба, называют окружностью заострения (рис. 5.10); ее диаметр
Формулой (5.23) пользуются также для нахождения толщины зуба
При проектировании зубчатых передач обычно стремятся, чтобы толщина зуба
|

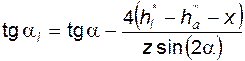 . (5.18)
. (5.18)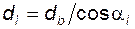 ; (5.19)
; (5.19) , или при
, или при (5.20)
(5.20)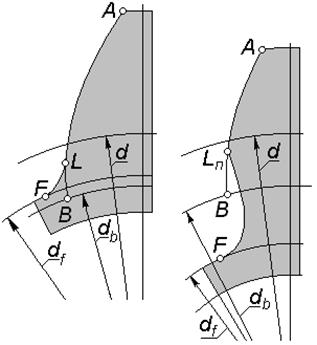
 называют коэффициентом наименьшего смещения исходного контура (коэффициентом наименьшего смещения).
называют коэффициентом наименьшего смещения исходного контура (коэффициентом наименьшего смещения).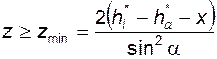 . (5.21)
. (5.21)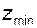 называют наименьшим числом зубьев свободным от подрезания (наименьшим числом зубьев).
называют наименьшим числом зубьев свободным от подрезания (наименьшим числом зубьев). ;
; 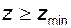 .
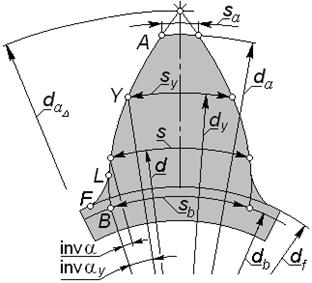
.
 по дуге окружности заданного диаметра
по дуге окружности заданного диаметра 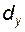 .
. ; (5.22)
; (5.22) ), угол профиля
), угол профиля 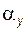 равен углу профиля исходного контура a, так как
равен углу профиля исходного контура a, так как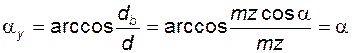 .
.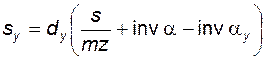 . (5.23)
. (5.23)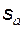 по дуге окружности вершин: при
по дуге окружности вершин: при 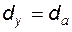 имеем
имеем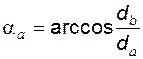 ; (5.24)
; (5.24)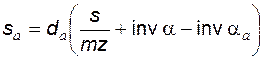 . (5.25)
. (5.25) находят из условия равенства нулю правой части выражения (5.25):
находят из условия равенства нулю правой части выражения (5.25): ; (5.26)
; (5.26) . (5.27)
. (5.27) по дуге основной окружности (основной толщины зуба); при
по дуге основной окружности (основной толщины зуба); при 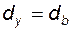 из (5.22) имеем
из (5.22) имеем  и тогда
и тогда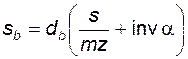 . (5.28)
. (5.28)



