Коэффициент перекрытия
На рис. 5.15 изображена пара взаимодействующих зубьев в двух положениях – в момент начала их участия в зацеплении в точке С момента входа какого-либо зуба в зацепление до момента выхода из него каждое из колес пары повернется на так называемый угол перекрытия
то каждая пара профилей входит в зацепление именно в тот момент, когда предыдущая пара (т.е. пара, ранее вступившая в контакт) выходит из зацепления. Для того чтобы процесс зацепления пары колес был непрерывным, необходимо, очевидно, чтобы каждая новая пара профилей вступала в контакт до выхода из зацепления предыдущей пары; это возможно только при Отношение
Для прямозубых колес вместо обозначения Можно показать, что для любого колеса пары
с учетом (5.42), (5.44) и (5.47), коэффициент перекрытия
Подытоживая сказанное, отметим, что коэффициент перекрытия характеризует непрерывность и плавность зацепления пары; теоретически работа передачи возможна при
|
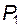и в момент окончания – в точке 
.
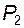и 
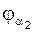. Если каждый из этих углов равен угловому шагу соответствующего колеса, т.е.
, 
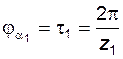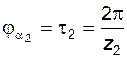, (5.47)
.
одинаково для обоих колес, его обозначают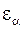 
и называют торцовым коэффициентом перекрытия; поскольку углы поворота зацепляющихся эвольвентных колес пропорциональны перемещению контактной точки по линии зацепления, то
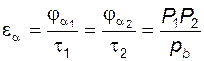. (5.48)
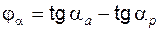, (5.49)
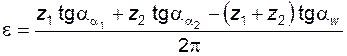. (5.50)
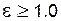, но на практике считают, что передача спроектирована верно, если для нее 
.
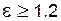