Свойства эвольвентного зацепления
Перечислим (без доказательства) наиболее важные свойства эвольвентного внешнего зацепления (рис. 5.3): 1) две эвольвенты при межосевом расстоянии
2) из (5.6) следует, что кинематика эвольвентного зацепления нечувствительна к погрешности межосевого расстояния; отметим, что таким свойством обладает только эвольвентное зацепление; 3) контактная точка Y в процессе зацепления перемещается по некоторой траектории, которую называют линией зацепления (можно также сказать, что линия зацепления является геометрическим местом контактных точек); в эвольвентном зацеплении такой линией является прямая
4) угол угол зацепления связан с межосевым расстоянием формулой
5) в зубчато-реечном эвольвентном зацеплении (рис. 5.4) рейка имеет прямолинейный профиль; при этом угол профиля рейки отметим, что сопряженность такого зацепления положена в основу геометрии и кинематики процесса нарезания эвольвентных зубьев инструментом реечного типа с прямолинейным профилем зуба; если инструментальная рейка перемещается вдоль своей начальной прямой со скоростью v, а нарезаемое колесо вращается с угловой скоростью w, то в процессе такого станочного зацепления будет сформирована эвольвента окружности диаметра
6) важным параметром эвольвентного колеса является основной шаг – расстояние
|

 всегда взаимно сопряжены, т.е. обеспечивают передачу вращения с постоянным передаточным отношением, равным
всегда взаимно сопряжены, т.е. обеспечивают передачу вращения с постоянным передаточным отношением, равным ; (5.6)
; (5.6)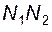 , касательная к обеим основным окружностям, она же в любой момент зацепления является и контактной нормалью;
, касательная к обеим основным окружностям, она же в любой момент зацепления является и контактной нормалью;
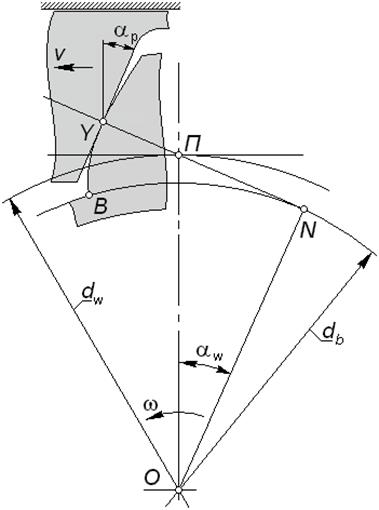

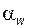 между межосевой линией и направлением касательной к профилям в контактной точке Y называют углом зацепления; в эвольвентном зацеплении угол
между межосевой линией и направлением касательной к профилям в контактной точке Y называют углом зацепления; в эвольвентном зацеплении угол 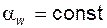 (никакое другое зацепление не обладает свойством постоянства угла
(никакое другое зацепление не обладает свойством постоянства угла 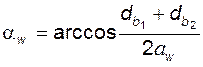 ; (5.7)
; (5.7) может быть любым, но каким бы он ни был, угол зацепления
может быть любым, но каким бы он ни был, угол зацепления  ;
;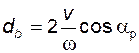 ; (5.8)
; (5.8)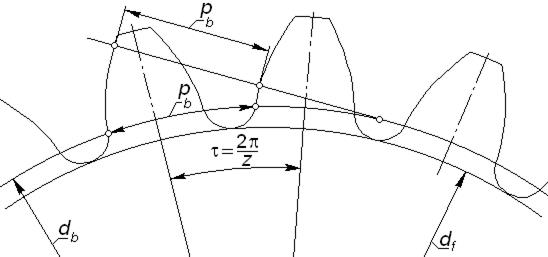
 между соседними одноименными эвольвентными профилями зубьев по дуге основной окружности; величину
между соседними одноименными эвольвентными профилями зубьев по дуге основной окружности; величину 


