Определение уравновешивающих сил и моментов методом Н. Е. Жуковского
Согласно принципу Даламбера все реально действующие на звенья механизма силы, дополненные уравновешивающими, а также инерционными силами и моментами, образуют равновесную систему. Согласно принципу возможных перемещений для такой системы сумма мгновенных мощностей всех сил и моментов в любой момент времени (и в любом положении механизма) равна нулю. И, что особенно важно, при расчетах без учета трения, т.е. в случае идеальных связей, реакции в кинематических парах в этом балансе мощностей не участвуют. Мощность каждого момента
где Мощность силы
Поскольку Произведение
здесь На равенстве (4.16) и основан метод Н. Е. Жуковского, реализация которого при вычислении уравновешивающих сил и моментов сводится к следующему (при условии, что план скоростей механизма уже построен в некотором масштабе 1) на плане скоростей отмечают точки приложения всех внешних сил (веса, инерции, полезного сопротивления); 2) к отмеченным точкам плана прикладывают соответствующие силы, повернутые на план скоростей с приложенными к указанным точкам силами интерпретируют как жесткий рычаг, шарнирно прикрепленный в полюсе 3) устанавливают правило знаков для выполненного построения; здесь нужно исходить из следующего: · знак момента любой силы в рычаге Жуковского должен совпадать со знаком ее мощности; · все силы, имеющие мощности одинакового знака, имеют в рычаге Жуковского моменты одинакового направления; таким образом, правило знаков можно установить по любой одной силе, для которой знак мощности достоверно известен; 4) составляют уравнение, которое, например, для механизма с одной степенью свободы и вращающимся начальным звеном имеет вид
Это уравнение имеет единственную неизвестную
|

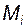 вычисляют по формуле
вычисляют по формуле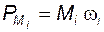 , (4.14)
, (4.14)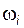 – угловая скорость звена, к которому приложен вращающий момент
– угловая скорость звена, к которому приложен вращающий момент 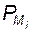 – величина алгебраическая, она положительна, если направления момента и угловой скорости совпадают.
– величина алгебраическая, она положительна, если направления момента и угловой скорости совпадают.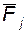 , приложенной в точке, скорость которой равна
, приложенной в точке, скорость которой равна 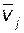 (рис. 4.11, а) находят как скалярное произведение указанных векторов
(рис. 4.11, а) находят как скалярное произведение указанных векторов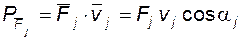 . (4.15)
. (4.15)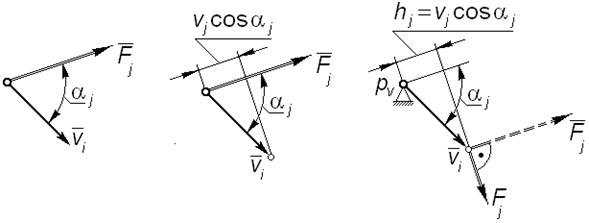 а б в
а б в
 – модули соответствующих векторов, т.е. величины заведомо положительные, то знак мощности
– модули соответствующих векторов, т.е. величины заведомо положительные, то знак мощности  полностью определяется знаком величины
полностью определяется знаком величины 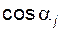 или правилом: мощность положительна, если угол
или правилом: мощность положительна, если угол 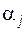 между векторами
между векторами  острый, и отрицательна, если этот угол тупой (очевидно, что мощность
острый, и отрицательна, если этот угол тупой (очевидно, что мощность 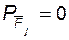 , если
, если  ).
).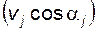 представляет собой проекцию вектора
представляет собой проекцию вектора 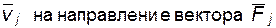 (рис. 4.11, б); но тогда мощность, определяемую равенством (4.15), можно рассчитать как момент силы
(рис. 4.11, б); но тогда мощность, определяемую равенством (4.15), можно рассчитать как момент силы  , повернутой относительно своего истинного направления на
, повернутой относительно своего истинного направления на 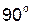 и приложенной к концу вектора
и приложенной к концу вектора  , относительно начала этого вектора
, относительно начала этого вектора ; (4.16)
; (4.16)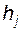 имеет размерность скорости.
имеет размерность скорости.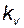 ):
):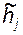 (в миллиметрах) относительно полюса плана
(в миллиметрах) относительно полюса плана  ;
;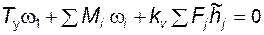 . (4.17)
. (4.17)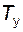 , которая легко определяется. Если полученное значение уравновешивающего момента положительно, то он направлен в сторону вращения начального звена.
, которая легко определяется. Если полученное значение уравновешивающего момента положительно, то он направлен в сторону вращения начального звена.


