Теорія ймовірності і математична статистика
Формули і таблиці З дисципліни Теорія ймовірності і математична статистика
Перестановка по k Pk = k! Розміщенння з n по k Ank = n!/(n-k)! Сполучення з n по k n- перестановок з повтореннями, Розміщення з n по k з повторенням Сполучення з повтореннями. Класичне означення ймовірності P(A + B) = P(A) + P(B) − P(A B) – сумісні P(A + B) = P(A) + P(B) - несумісн і P(AB)=P(A)×P(B/A) – залежні P(AB)=P(A)×P(B) – незалежні формула повної ймовірності: Ф ормула Байеса: Повторення експерименту. Формула Бернуллі Локальна теорема Лапласа Формула Пуассона Інтегральна теорема Лапласа
Найвірогідніше число здійснення події np-q≤k0≤np+p, де q=1-p. Теорема Бернуллі про стійк. відн. частот події Основні числові характеристики ВВ Матсповідання ДВВ: Матсповідання НВВ: Дисперсія ДВВ: Дисперсія НВВ: Середнє квадратичне відхилення: другий початковий момент ДВВ: другий початковий момент НВВ: В інженерній практиці D(X) визначають за допомогою другого початкового моменту: D(X)=α2-M(Х2), тобто
|
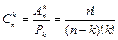
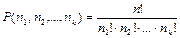
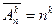
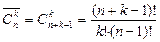
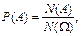P(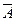 
) = 1 − P(A).
;
;
;
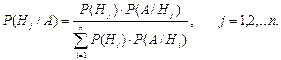
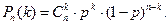
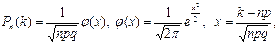
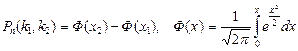
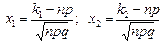
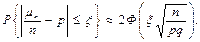
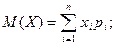
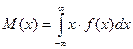
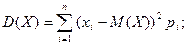
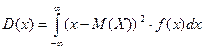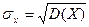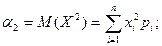
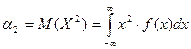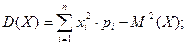- для ДВВ;
