Геометрические параметры зубчатых колес
Основные размеры зубчатого колеса определяемые из рассмотрения станочного зацепления нарезаемого колеса с производящей рейкой (рис. 4.1) следующие. Делительный окружной шаг зубьев р = π m. (4.1)
Радиус делительной окружности r определим из равенства 2π r = р 0 z:
Рис. 4.1. Станочное зацепление Радиус основной окружности rb. Линия станочного зацепления касается основной окружности нарезаемого колеса. Из треугольника ОМП0(рис. 4.1)
Радиус окружности впадин rf. Поверхность впадин нарезаемого колеса формируется вершиной зуба производящей рейки, следовательно, радиус окружности впадин будет (рис. 4.1)
где
Для колёс, нарезаемых без смещения (х= 0), Делительная толщина зуба S. Толщина зуба S по делительной окружности равна ширине впадины рейки по начальной прямой (рис. 4.2).
Таким образом,
У колес, нарезаемых без смещения,
Рис. 4.2. К определению делительной толщины зуба Толщина зуба на произвольной окружности. Из рис. 4.3 можно записать
где j – половина угловой толщины зуба по делительной окружности; j у – половина угловой толщины зуба на окружности радиуса ry.
Рис. 4.3. Определение толщины зуба на произвольной окружности Выразив угловую толщину зуба через окружную, получим
Угол профиля зуба
|

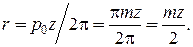 (4.2)
(4.2)
 (4.3)
(4.3)
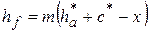 или
или (4.4)
(4.4)
 .(4.5)
.(4.5)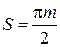 .
.
 ,
,
 или
или . (4.6)
. (4.6) на окружности радиуса ry можно определить из треугольника ОМК:
на окружности радиуса ry можно определить из треугольника ОМК: . (4.7)
. (4.7)


