Цепи, состоящие из резисторов
При последовательном соединении резисторов их сопротивления складываются
Доказательство: Так как общая разность потенциалов равна сумме её составляющих:
А из закона Ома падение напряжения
при этом из закона сохранения заряда, через все резисторы идёт одинаковый ток
Делим всё на ток
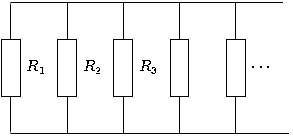
При параллельном соединении резисторов складываются величины, обратные пропорциональные сопротивлению (то есть общая проводимость
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находя общее(искомое) сопротивление. Доказательство: Так как заряд при разветвлении тока сохраняется, то: Из закона Ома ток Делим всё на U и получаем общую проводимость Пример
Схема состоит из двух параллельно включённых блоков, один из них состоит из последовательно включённых резисторов Для расчёта таких цепей из резисторов, которые нельзя разбить на блоки последовательно или параллельно соединённые между собой, применяют правила Кирхгофа. Иногда для упрощения расчётов бывает полезно использовать преобразование треугольник-звезда и применять принципы симметрии.
|


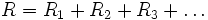
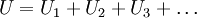
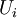 на каждом сопротивлении
на каждом сопротивлении 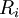 равно:
равно: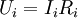
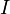 , поэтому подставляя в формулу для суммы напряжений закон Ома, записываем:
, поэтому подставляя в формулу для суммы напряжений закон Ома, записываем: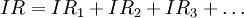
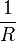 складывается из проводимостей каждого резистора
складывается из проводимостей каждого резистора 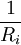 )
)
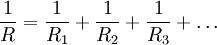
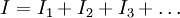
 через каждый резистор равен:
через каждый резистор равен: 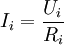 , но разность потенциалов на всех резисторах будет одинакова, поэтому перепишем уравнение суммы токов:
, но разность потенциалов на всех резисторах будет одинакова, поэтому перепишем уравнение суммы токов: 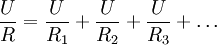
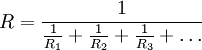
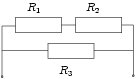
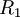 и
и  , общим сопротивлением
, общим сопротивлением 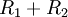 , другой из резистора
, другой из резистора 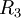 , общая проводимость будет равна
, общая проводимость будет равна 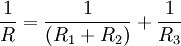 , то есть общее сопротивление
, то есть общее сопротивление 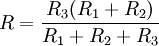 .
.


