Понятие индексов, их виды
Тема 1.6 Индексы 1.Понятие индексов, их виды 2.Индексы индивидуальные и общие. Формы индексов: агрегатная, среднегармоническая, среднеарифметическая. Их расчет, правила построения и условия применения 3.Индексы цепные и базисные 4. Индексы переменного и постоянного состава, индекс структурных сдвигов, их взаимосвязь 5. Использование индексного метода при анализе взаимосвязей экономических явлений
Учебное занятие № 12 Понятие индексов, их виды Индексный метод - один из самых распространенных методов статистического анализа экономических явлений. С помощью индексов изучаются: – народное хозяйство в целом и его отдельные отрасли, – деятельность предприятий, объединений и др.; – выявляется динамика развития социально-экономических явлений, анализируется выполнение планов или норм; –определяется влияние отдельных факторов на общий результат, вскрываются резервы производства. Индексом в статистике называется относительный показатель, характеризующий соотношение во времени, по сравнению с планом уровней социально-экономических явлений. Так как индекс - относительный показатель, то он всегда получается при соотношении двух величии: отчетной (или текущей) и базисной. Различают следующие виды индексов: –если за базу сравнения берется уровень явления за какой-то прошлый период времени, получают динамические индексы; –если за базу сравнения берется уровень явления на другой территории, получают территориальные индексы; –если за базу сравнения берется какой-либо нормативный уровень, получают индексы выполнения плана, индексы выполнения норм и т. д. Как и всякая относительная величина, индексы выражаются: –в виде коэффициентов, если за основание принимается единица; – в виде процентов, если за основание принимается сто. В индексах, характеризующих изменение явления в динамике, различают два периода: –базисный период – это начальный период, т.е. период, с которым производится сравнение; –текущий (отчетный) период – это период, уровень которого сравнивается. В формулах текущие данные помечают единицей, стоящей чуть ниже буквенного обозначения величины (р1).Данные, которые используются в качестве базы сравнения, помечаются нулем (р0).
2.Индексы индивидуальные и общие. Формы индексов: агрегатная, среднегармоническая, среднеарифметическая. Их расчет, правила построения и условия применения Индивидуальные индексы рассчитываются для отдельных элементов сложного явления и обозначаются латинской буквой i. Общие индексы рассчитываются для всего сложного явления в целом и обозначаются буквой I. Обозначения анализируемых величин в статистике: q - количество единиц данного вида произведенной(реализованной) продукции; p - цена единицы изделия; t - трудоемкость единицы изделия; w - выработка продукции на одного работающего; Z - себестоимость единицы изделия. Для исчисления индивидуальных индексов применяются следующие формулы: – индивидуальный индекс физического объема
где q1- количество произведенной или реализованной продукции в текущем (отчетном) периоде; q0- количество произведенной или реализованной продукции в базисном периоде.
– индивидуальный индекс цен
где р1- цена продукта в текущем (отчетном) периоде; р0- цена продукта в базисном периоде.
– индивидуальный индекс себестоимости
где Z1- себестоимость продукта в текущем (отчетном) периоде; Z0 - себестоимость продукта в базисном периоде.
– индивидуальный индекс трудоемкости
где t0 - трудоемкость изготовления изделия в базисном периоде; t1 – трудоемкость изготовления изделия в текущем (отчетном) периоде.
– индивидуальный индекс выработки продукции на 1работающего
где w1 - выработка продукции на 1 работающего в текущем (отчетном) периоде; w0 - выработка продукции на 1 работающего в базисном периоде.
Основной формой общих индексов являются агрегатные индексы. Каждый общий индекс состоит из двух элементов: –индексируемые величины, изменение которых должен отразить индекс; –показатели, которые служат соизмерителями (весами). При их помощи несоизмеримые показатели индекса приводятся в сопоставимый вид. Веса – это одинаковые величины в числителе и знаменателе индекса. Произведение каждой индексируемой величины на соизмеритель (вес) должно давать определенную экономическую категорию (стоимость произведенной продукции = цена x количество) Значение индексируемой величины всегда изменяется: отчетное значение сопоставляется с базисным. Конкретное название индекса дается всегда по индексируемой величине. Агрегатные индексы: – агрегатный индекс цен Iр рассчитывается по формуле
где ро, р1 - цена каждого вида продукции соответственно в базисном и текущем периодах; q1- количество каждого вида продукции в отчетном периоде (вес индекса). Индекс цен характеризует среднее изменение цен на продукцию (товары), проданные в отчетном периоде. Числитель индекса характеризует объем стоимости произведенной или реализованной продукции (товарооборот) отчетного периода в фактических ценах, а знаменатель – тот же объем стоимости произведенной, реализованной продукции (товарооборота) в ценах базисного года. Разность между числителем и знаменателем (∑р1q1 - ∑роq1) характеризует абсолютную сумму выигрыша (проигрыша) от снижения (роста) цен –агрегатный индекс физического объема рассчитывается по формуле
где qо - количество каждого вида продукции в базисном периоде.
Индекс физического объема продукции характеризует динамику продукции в неизменных (одинаковых) ценах. Разность между числителем и знаменателем индекса (∑q1ро - ∑ qоро) характеризует абсолютный прирост валовой продукции в неизменных ценах - агрегатный индекс стоимости произведенной или реализованной продукции, или товарооборота, Iрq рассчитывается по формуле
где роqо и р1q1 - стоимость произведенной или реализованной продукции, или товарооборота в базисном и отчетном периодах соответственно. - агрегатный индекс себестоимости, Iz рассчитывается по формуле
где Z1 и Zо - себестоимость каждого вида продукции соответственно в текущем и базисном периодах. Числитель индекса характеризует затраты в производстве в отчетном периоде на сопоставимую продукцию, знаменатель – те же затраты в производстве, которые были бы, если бы себестоимость оставалась на уровне базисного периода. Разность между числителем и знаменателем характеризует экономию от снижения себестоимости одноименной продукции или перерасход, если себестоимость выросла (∑Z1q1 - ∑ Zоqо) Агрегатные формы индексов взаимосвязаны. Это позволяет по известным двум индексам находить третий индекс. Так как стоимость товаров – это произведение цены на количество товаров (рxq), индекс фактического стоимостного объема произведенной или реализованной продукции, или товарооборота Iрq должен равняться произведению индекса цен Iр на индекс количества Iq.
или
Большим достоинством агрегатных индексов является то, что они дают возможность определить не только относительные изменения явления, но и найти абсолютные значения изменений. Если из числителя каждого агрегатного индекса вычесть его знаменатель, то можно получить величины абсолютных приростов: – общей стоимости произведенной или реализованной продукции, или товарооборота
в том числе за счет различных факторов: а) за счет изменения уровней цен
б) за счет изменения физического объема продукции
При этом должно соблюдаться следующее равенство
Средний арифметический индекс физического объема рассчитывается по формуле
Результат расчета должен получиться тот же, что и при расчете агрегатного индекса физического объема. Для расчета среднего арифметического индекса необходимо иметь данные об индивидуальных индексах (iq) и стоимости продукции в базисном периоде (poqo) по отдельным ее видам. Средний гармонический индекс цен рассчитывается по формуле
Результат расчета должен получиться тот же, что расчет агрегатного индекса цен. Учебное занятие № 13
|

 (1)
(1)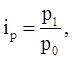 (2)
(2) (3)
(3)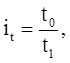 (4)
(4)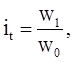 (5)
(5)
 (6)
(6) (7)
(7)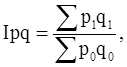 (8)
(8)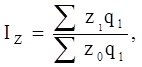 (9)
(9)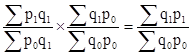 (10)
(10) (11)
(11)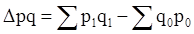 (12)
(12) (13)
(13)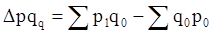 (14)
(14) (15)
(15) (16)
(16) (17)
(17)


