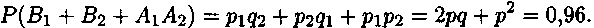Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее щести очков, равна… 1/6
Таблица 1 УIX 1 2 3
;4 0,1 1, 5 0,12 5 0,2 0,22 0,1. 6 0,01 0 0,1
Таблица 2 УIX 1 2 3 5
;4 0,1 0,15 0,1 0,02 5 0,13 -0,2 0,15. 0,05 6 0,01 0,03 0,03 0,04
Таблица 3 УIX 1 2 3
4 0,42 0,51 0,15. 6 0,1 0,15 0,1 8 0,01 0,03 0,03 10 0,05 0,02 0,04 все Кроме них Двумерную величину обозначают через (X, У); каждая из величин X и Y называется.... компонента
Законом распределения двумерной случайной величины (X, У) называют множество возможных пар чисел (хi,уj) и их вероятностей p(xi,yj) Верно
закон распределения двумерной случайной величины (X, У) имеет вид прямоугольной таблицы из элементов pij, где pij=P(X=xi:Y=yj) верно
Сумма всех вероятностей в законе распределения равна единице: Верно
Из того, что Д(Х)+Д(У)¹Д(Х+У) можно сделать вывод о том, что случайные величины являются независимыми. верно Корреляционным моментом случайных величин X и У (или ковариацией) называется математическое ожидание произведений их отклонений: цху = Cov (X, У) = М{[Х - M(X)][Y -M(Y)]} верно
Корреляционный момент двух зависимых случайных величин X и Y равен нулю неверно Коэффициентом корреляции случайных величин X и У называется отношение их ковариации (корреляционного момента) к произведению средних квадратических отклонений этих величин:
Верно
Коэффициент корреляции имеет свойство: его абсолютная величина не превосходит единицы │rxy│;
Две случайные величины X и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля
две коррелированные случайные величины (т.е. при гху № 0) являются также и зависимыми неверно
две зависимые величины могут быть как коррелированными, так и некоррелированными верно
коэффициент корреляции близок к нулю; это означает, что случайные величины X и Y коррелированы. Неверно
Линейная средняя квадратическая регрессия Y на X имеет вид
Верно
Коэффициент b = rхуsу/sх называют коэффициентом регрессии Y на X Верно
Сумма всех вероятностей в законе распределения равна нулю Неверно
Две случайные величины X и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) равен нулю
Неверно
Законы распрелелднмия
медиана случайной величины X, имеющей равномерное распределение R(2;8) равна:
Вероятность Р(Х.>7) случайной величины X, имеющей равномерное распределение R(2;8) равна:
Вероятность Р(Х.=7) случайной величины X, имеющей равномерное распределение R(2;8) равна:
Вероятность Р(Х.>10) случайной величины X, имеющей равномерное распределение R(2;8) равна 0
Вероятность Р(Х<1) случайной величины X, имеющей равномерное распределение R(2;8) равна 0
Вероятность Р(3<Х<7) случайной величины X, имеющей равномерное распределение R(2;8) равна 2/3
математическое ожидание случайной величины X, имеющей равномерное распределение R(2;8) равно 5
Функцией распределения случайной величины X называется функция F(x), определяющая вероятность того, что случайная величина X примет значение, меньшее х: F(x) = Р(Х < х). верно Случайная величина называется непрерывной, если ее функция распределения есть непрерывная кусочно-дифференцируемая функция с непрерывной производной. Верно Производная от функции распределения непрерывной случайной величины X называется плотностью распределения вероятностей X: f(x) = F'(x). Верно
Интеграл с переменным верзним пределом от плотности распределения вероятностей f(x) непрерывной случайной величины X называется функцией распределения F(x):
Вероятность того, что непрерывная случайная величина X не примет значение на интервале (а,b), определяется по формуле Р(а < X < b) = Верно
Функция распределения является неубывающей, т.е. F(x2) Верно
Область значений функции распределения лежит на отрезке [0,1]: О
Если возможные значения случайной величины находятся на интервале (а, b), то F(x) = 0 при х<; а и F(x) = 1 при х > b. верно
Вероятность того, что случайная величина X принимает значения, заключенные внутри интервала (а, b ), равна разности значений функции распределения на концах этого интервала: Р(а £ X<b)=F(b)- F(a). Верно Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю. Верно Если возможные значения непрерывной случайной величины X расположены на всей числовой оси, то lim F(x) = 0, lim F(
x®-¥ x®¥
Плотность распределения не является неотрицательной функцией: Неверно Несобственный интеграл от плотности распределения в пределах интегрирования по всей числовой оси равен единице:
Математическим ожиданием непрерывной случайной величины X, называется определенный интеграл: М(Х) = Верно
Дисперсией непрерывной случайной величины X называется математическое ожидание квадрата ее отклонения: D(X) = Среднее квадратическое отклонение случайной величины определяется по формуле
Верно
Классич опр вероя
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна… 2/6
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет «четверка», равна…1/6
Игральная кость бросается два раза. Тогда вероятность того, что на верхней грани оба раза выпадет «четверка», равна…1/36
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани не выпадет «четверка», равна…5/6
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырех очков, равна…1/2 Игральная кость бросается два раза. Тогда вероятность того, что на верхней грани оба раза не выпадет «тройка», равна…25/36
Бросают 2 монеты. События А - «герб на первой монете» и В - «цифра на второй монете» являются… сомвестные и независимые
Бросают 2 игральные кости. События А - «шестерка на первой кости» и В - «двойка на второй кости» являются… совместные и независимые
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет менее четырех очков, равна… ½
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее щести очков, равна… 1/6
Данная формула … полной вероятнот
Формула числа сочетание используют если выборка: без повторения и без упорядочения
Противоположным событием
Суммой двух событий называют событие, состоящее в том, что происходит …или одно событие или другое событие
Произведением двух событий называют событие, состоящее в том, что происходит…и одно событие и другое событие
Абонент забыл последнюю цифру номера телефона своего знакомого и набрал ее наугад. Вероятность того, что он набрал правильный номер, равна 0,5
Неверно
Вероятность того, что студент сдаст каждые из 3-х экзаменов сессии на отлично равна соответственно 0,4;0,5;0,1.Получение отличных оценок на этих экзаменах события независимые. Вероятность того, что студент сдаст на отлично все 3 экзамена, равна…0,02
Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна0,2. второй 0,1. Обращение клиентов события независимые. Вероятность того, что в течение года в страховую компанию обратится хотя бы один из этих клиентов, равна…0,28
В коробке 4 стандартных и 2 бракованных детали. Подряд вынимают 2 детали, при этом не возвращают их обратно в коробку. Вероятность того, что обе вынутые детали бракованные, равна..1/15
следующий нтеграл от плотности распределения f(x) непрерывной случайной величины
Если 2 события не могут произойти одновременно, то они называются … несовместными
Если А={1,2,3,4,5 } и В={4,5,6} то
Если А={1,2,3,4,5 } и В={4,5,6} то
Корреляц анализ
Если известно, что существует коэффициент корреляции двух случайных величин ξ и η ρ(ξ,η), причем η=-2ξ+1; то из этого следует, что:… ρ(ξ,η) = 1 какое из перечисленных ниже свойств не является верным для функции распределения случайного вектора (ξ1, ξ2): 1.
2. 3. 4.
Только 2+ + Если Mξ=5, Dξ=2, то будет справедлива следующая оценка…: P(|ξ-5| ≥ 10) ≤ 0.02
Случайная величина имеет распределение Пуассона с параметром λ = 5, если
Вероятность того, что в небольшом числе n независимых испытаний с постоянной вероятностью p появления события в каждом из них событие А наступит m раз определяется по формуле …Бернулли
Попарно несовместные наблюдаемые события, в сумме составляющие достоверное событие называются …полная группа событий
Событие, которое в данных условиях никогда не происходит - …невозможное
Произведение двух событий - это событие, состоящее в …одновременном их появлении
События со всеми общими составляющими их элементами - …равносильные,
Одновременно бросают 6 кубиков. Вероятность того, что сумма очков на кубиках меньше 6 составляет …0
Одновременно бросают 6 кубиков. Событие состоящее в том, что сумма очков на кубиках меньше 6 является …невозможным
Проверка гипотез о парамет
Оценкой математического ожидания является… Средняя арифметическая –X
Оценкой является несмещенной, если… Математическое ожидание оценки равно значению оцениваемого параметра
Математическое ожидание постоянной величины равно… Этой величине
Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …(8,5; 11,5)
Если основная гипотеза имеет вид Н0:m=m0, то конкурирующей может быть гипотеза …Н1:m≠m0 Н1:m>m0
Точечная оценка дисперсии по выборке объёма n=11 нормального распределения равна 20. Тогда исправленная дисперсия равна …22
В результате измерений некоторой величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 11, 13, 15. Тогда несмещенная оценка дисперсии измерений равна…4
Если все элементы выборки учвеличить на одно и то же число то дисперсия не изменится верно
Если все элементы выборки учвеличить на одно и то же число то дисперсия увеличится на это число верно
Если все элементы выборки учвеличить на одно и то же число то дисперсия не изменится верно
Если все элементы выборки умножить на одно и то же число то дисперсия не изменится не верно
Если все элементы выборки умножить на одно и то же число то дисперсия умножится на квадрат этого числа верно Если все элементы выборки умножить на одно и то же число то выборочная средняя умножится на это число … верно
Если все элементы выборки умножить на одно и то же число то выборочная средняя не изменится … не верно
Если все элементы выборки увеличить на одно и то же число то выборочная средняя не изменится … не верно
Если основная гипотеза имеет вид Н0:m=15, а интервальная оценка математического ожидания нормального распределения имеет вид (7,5;12,5) то надо принять альтернативную гипотезу верно
Если основная гипотеза имеет вид Н0:m=15, а интервальная оценка математического ожидания нормального распределения имеет вид (7,5;12,5) то надо принять основную гипотезу… неверно
Если основная гипотеза имеет вид Н0:m=11,5, а интервальная оценка математического ожидания нормального распределения имеет вид (7,5;12,5) то надо принять основную гипотезу … верно
Однофакторный дисперсионный анализ предназначен для проверки гипотезы о равенстве средних нескольких выборок верно
Выборочное среднее имеет пормальное распределение при известной дисперсии Верно
Выборочное среднее имеет t-распределение Стьюдента при неизвестной дисперсии Верно
t-распределение Стьюдента при достаточно больших n близко к нормальному распределению верно
случайные величины
Случайная величина имеет нормальное распределение с параметрами a=3,σ=1, если плотность распределения имеет вид:
Известно, что Х - случайная величина, имеющая дисперсию Д(х)=1/5, тогда дисперсия случайной величины У=7Х+1 равна:… 49/5
Известно, что Х - случайная величина, имеющая матожидание М(х)=3, тогдаматожидание случайной величины У=7Х+1 равна: … 22
Если ξ - случайная величина, имеющая нормальное распределение с параметрами а=4 и σ=2;, то стандартной нормально распределенной случайной величиной будет случайная величина η: … η = (ξ-4)/2
Функция распределения одномерной случайной величины дискретного типа, принимающей конечное число значений, обладает следующим свойством …имеет счетное число точек разрыва;… имеет промежутки постоянства значений функции;
Биномиальная схема - модель, соответствующая …последовательности испытаний с 2 исходами в каждом; исходы каждого испытания независимы…последовательности независимых испытаний с двумя исходами в каждом;
Какие события взаимоисключают друг друга и обязательно происходят в результате любого опыта:… элементарные;
Случайная величина имеет распределение Пуассона с параметром λ = 5, если… \
В ящике в 7 раз больше белых шаров, чем черных. Наугад выбирается один шар. Вероятность того, что он будет черным равна:… 1/8
Для независимых событий А и В Р(А+В) равна:… Р(А) + Р(В) - Р(А)Р(В);
Какие из приведенных соответствий являются законами распределения xi 0 10 20 30 40 pi 0,1 0,2 0,4 0,2 0,1
Задан закон распределения xi 0 1 2 3 4 pi 0,1 0,2 0,4 0,2 р5 Значение р5=… 0,1
математическое ожидание случайной величины X, заданной следующим распределением равно: …2,6 X -5 2 3 4 6 р 0,1 0,2 0,3 0,3 0,1.
Найти дисперсию случайной величины X, заданной следующим распределением: X -5 2 3 4 6 р 0,1 0,2 0,3 0,3 0,1. …..7,64
Математическое ожидание числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0,015, причем куплено 200 билетов. равно...3
математическое ожидание случайной величины X, имеющей равномерное распределение R(21) равно:..4,5
Математическое ожидание случайной величины X, имеющей биномиальное распределение Bi(10; 0.5) равно: 5
Дисперсия случайной величины X, имеющей биномиальное распределение Bi(20; 0.5) равна:
Значение Р(Х=0) случайной величины X, имеющей биномиальное распределение Bi(4; 0.5) равно … 1/16
медиана случайной величины X, имеющей равномерное распределение R(2;18) равна … 10
Вероятность Р(Х.=7) случайной величины X, имеющей равномерное распределение R(1;14) равна … 0
Вероятность тго,что непрерывная случайная величина примет какое-то фиксированное значение равна нулю … верно
Дисперсия случайной величины характеризует её положение…. Неверно
Дисперсия суммы случайных величин равна сумме их дисперсий.. неверно
Значение Р(Х=1) случайной величины X, имеющей биномиальное распределение Bi(4; 0.5) равно: 1/4
Значение Р(Х=1) случайной величины X, имеющей биномиальное распределение Bi(4; 0.5) равно значению Р(Х=3) верно
Статистичкское распределение
Выборочной модой М0 называется варианта имющая … частоту наибольшую
Выборочной медианой те называется варианта, которая делит вариационный ряд на... равные части … две
статистическим распределением выборки (рядом распределения) называется состветствием между различными значениями и их …частотами
вариационным рядом называется выборка упорядоченная по …… неубыванию 1, 3, 2, 2, 2 для данной выборки выборочное среднее равно … 2
1, 3, 2, 2, 2 для данной выборки значение моды равно… 2
1, 3, 2, 2, 2 для данной выборки значение медианы равно … 2
1, 3, 2, 2, 2 для данной выборки значение исправленной дисперсии равно … 0,5
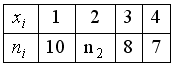
Из генеральной совокупности извлечена выборка объема n=50:
Из генеральной совокупности извлечена выборка объема n=30:
Мода вариационного ряда 1, 4, 4, 5, 6, 8, 9 равна … 4
В результате измерений (без систематических ошибок) получены следующие результаты (в мм): 36, 38, 40. Тогда несмещенная оценка дисперсии измерений равна…8/2
В результате измерений получены следующие результаты (в мм): 11, 13, 15. Тогда выборочная дисперсии измерений равна…8/3
Точечная оценка дисперсии по выборке объёма n=11 нормального распределения равна 20. Найдите значение исправленной дисперсии …22
Если основная гипотеза имеет вид Н0:m=m0, то альтернативной может быть гипотеза …Н1:m≠m0 …Н1:m>m0
. Если точечная оценка математического ожидания нормального распределения равна 10, то его интервальная оценка может иметь вид …(8,5; 11,5)
Вероятность успеха в 10 независимых испытаниях, по схеме Бернулли, равна 0,8. Тогда дисперсия числа появлений этого события имеет значение…1,6
/Если из генеральной совокупности извлечена выборка объема n=40:
Мода вариационного ряда 1, 4, 4, 5, 6, 8, 9, 10, 11 равна… 4
Из генеральной совокупности извлечена выборка объема n=30:
Цепи Маркова
Марковская цепь задана матрицей переходов
Марковская цепь задана матрицей переходов
если в момент t=10 система находилась в состоянии (0;0;1), то это означает, что система находилась в состоянии S3 … верно
если в момент t=10 система находится в состоянии S1, то это означает, что вектор состояний системы имеет вид (1;0;0) … верно
Марковская цепь S1; S2 задана матрицей переходов
Марковская цепь задана графом
Дана марковская цепь, её матрица переходов имеет вид
Марковская цепь задана матрицей переходов Дана марковская цепь,, её матрица переходов имеет вид
Вероятность Pij(n) может быть найдена по формуле, называемой...:
… равенство Маркова
матрица, составленная из условных вероятностей перехода будет иметь вид:
… верно
матрица, составленная из условных вероятностей перехода будет иметь вид:
Эта матрица называется матрицей… перехода системы последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. При этом условная вероятность pij(s) того, что в s -ом испытании наступит событие Aj при условии, что в (s - 1) - ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний.Называется … цепью Маркова
Процесс, протекающий в системе, называется ...марковским… ой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
цепь Маркованазывается ..., если условная вероятность pij перехода системы из состояния i в состояние j не зависит от номера испытания. Однородной
Квадратные матрицы, элементы которых нетрицательны и суммы элементов по каждой строке которых равны единице, называются … стохастической
Марковская цепь задана матрицей переходов
Числовые характеритсики
Случайная величина Y=4x+2, при этом математическое ожидание Х равно3. Математическое ожидание случайной величины Y равно … 14
Случайная величина Y=3x+5, при этом дисперсия Х равна 2.Дисперсия случайной величины Y равна … 23
Парный коэффициент корреляции изменяется в пределах:… Парный коэффициент корреляции между признаками равен 1. Это означает …. Наличие функциональной связи
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности: М(Х) =х1р1+х2р2+…+хпрп =∑ хiрi Верно
Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно (в особенности для большого числа испытаний).... значений случайной величины …. Среднему арифметическому
... дискретной случайной величины называется сумма произведений квадратов отклонений всех ее возможных значений от математического ожидания на их вероятности: Д (Х) = (х1-mx)2р1+(х2-mx)2р2+…+(хп-mx)2рп = ∑ (хi -mx)2рi… дисперсией математическое ожидание квадрата отклонения называется … дисперсией
Средним квадратическим отклонением sх случайной величины X (стандартом) называется...из ее дисперсии…. квадратный корень
Математическое ожидание характеризует некоторое... значения вокруг которого группируются все значения случайной величины… среднее
... есть мера разброса (рассеяния) значений случайной величины… дисперсия
Пусть Х- произвольная случайная величина, М(х) её математическое ожидание, e>0 произвольное число. Тогда справедливо неравенство
Называемое первое неравенство Чебышева
Пусть Х- произвольная случайная величина, М(х) и Д(х) её математическое ожидание и дисперсия, e>0 произвольное число. Тогда справедливо неравенство
Пусть Х- произвольная случайная величина, М(х) и Д(х) её математическое ожидание и дисперсия, e>0 произвольное число. Тогда справедливо неравенство
Математическое ожидание постоянной величины С равно … этой постоянной
Постоянный множитель... выносить за знак математического ожидания: М(СХ) = СМ(Х). Можно
Математическое ожидание суммы случайных величин равно... их математических ожиданий … сумме
Математическое ожидание произведения независимых случайных величин равно... их математических ожиданий: Произведению
Дисперсия постоянной величины С равна…. Нулю
Постоянный множитель можно выносить за знак дисперсии, возводя его … в квадрат
Дисперсия суммы независимых случайных величин равна их дисперсий … сумме
Случайная величина Z=4X+2Y-1, при этом математическое ожидание Х равно 3, математическое ожидание Y равно 5. Тогда математическое ожидание случайной величины Z равно …21
В кабеле длиной 6 м пробой одинаково возможен в любом месте, какова вероятность того, что пробой произошел на расстоянии равном точно одному метру от начала? В данном примере мерой m служит длина. В роли W выступает весь отрезок, длиной 6 м, W={x; x Какова вероятность выпадения не менее 5-ти очков при одном бросании кубика? Бросание кубика может иметь 6 равновозможных исходов: W ={vi; i=1,6}, vi-событие, состоящее в том, что выпало i очков, N(W)=6, А- искомое событие, А={v5, v6}, N(A)=2, значит Р(А)= Какова вероятность того, что число очков, выпавших при двух бросаниях игральной кости будет отличатся меньше, чем на 2 единицы?
Производится одновременно по одному выстрелу из двух орудий, в силу конструктивных особенностей вероятность попадания в данную цель для первого орудия равна 0,9, а для второго 0,8. Найдите вероятности событииz А=(попали оба);
Р(А)=0,9*0,8=0,72
Производится одновременно по одному выстрелу из двух орудий, в силу конструктивных особенностей вероятность попадания вв данную цель для первого орудия Р(Е!)равна 0,9, а для второго Р(Е»)= 0,8. и для третьего Р(Е3)=0,7. Найдите вероятности события А3=(попали все); Р=0,9*0,8*0,7=0,504
В ящике лежит 11 деталей, 3 из них нестандартные. Из ящика дважды берут по одной детали, не возвращая их обратно. Найти вероятность того, что во второй раз из ящика будет извлечена стандартная деталь, если в первый раз была извлечена нестандартная деталь. Р (В/А) = 0,8.
В условиях когда вероятности попадания при выстреле для первого стрелка равна 0,9, для второго 0,8, для третьего 0,7 найти вероятность поражения цели (хотя бы одного попадания) при залповой стрельбе). Р(А) = 1 – q1*q2*q3= 1 - 0,006 = 0,994
На выполнение заказа направлены 4 автомобиля. Вероятность нахождения каждой из машин в исправном состоянии равна 0,8. Найти вероятность того, что в работе участвует хотя бы один из выделенных для этого автомобилей. Р(А) = 1-q4 = 1- 0,24 = 0,9984
Инвестор решил вложить свои средства поровну в два проекта, каждый из которых принесет ему прибыль в размере 100%. Вероятность того, что любой из проектов оправдает ожидания, равна 0,8. Какова вероятность того, что в итоге инвестор по меньшей мере ничего не потеряет?
Партия объемом 10 тонн семян составлена из 5 тонн семян с всхожестью 0,9 и 5 тонн с всхожестью 0,8. Какова всхожесть семян во всей партии? Р(А)= ½*0,9 + ½*0,8=0,85
Испытания проводятся до тех пор, пока событие А не произойдет заданное количество раз. Какова вероятность того, чтобы выпадение 5-ти очков произошло три раза потребуется серия из: А- трех; В- четырех; С- пяти; Д- шести бросании кубика?
Задан закон распределения xi 0 1 2 3 4 pi 0,1 0,2 0,4 0,2 р5 Найдите значение р5 р5=1-0,1-0,2-0,4-0,2=0,1
В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20 р., два выигрыша по 10 р. и 10 выигрышей по 1 р. Найдите закон распределения случайной величины X возможного выигрыша на один билет
Возможные значения X: x1=20, х2=10, хз=1, х4=0. Соответственно их вероятности равны: p1=1/100=0,01, p2=2/100=0,02, рз=10/100=0,1, Р4=(100 – 1-2-10)/100= = 0,87. Таким образом, искомый закон распределения имеет вид X 20 10 1 О Р 0,01 0,02 0,1 0,87.
|

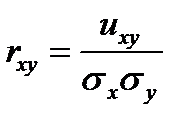
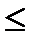 1 верно
1 верно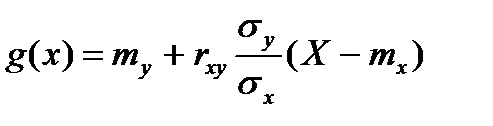
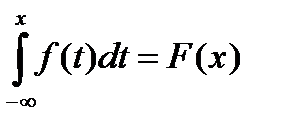 верно
верно f(x)dx=F(b)-F(a).
f(x)dx=F(b)-F(a).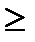 F(x1) при x2>x1
F(x1) при x2>x1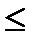 F(x)
F(x) 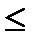 1. верно
1. верно x) = 1. верно
x) = 1. верно верно
верно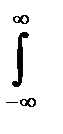 xf(x)dx.
xf(x)dx.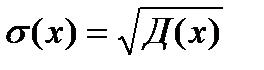
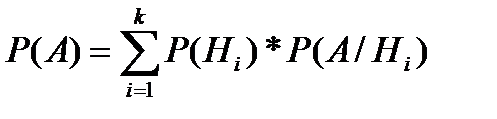 называется формулой
называется формулой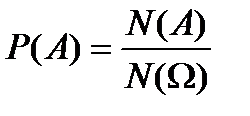 данная формула называется формулой… классической вероятностью
данная формула называется формулой… классической вероятностью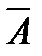 называют событие состоящее в том, что…событие А не происходит
называют событие состоящее в том, что…событие А не происходит равен …1
равен …1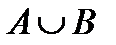 = …{1,2,3,4,5,6}
= …{1,2,3,4,5,6}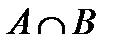 =… {4,5 }
=… {4,5 }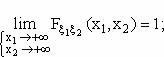
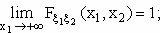
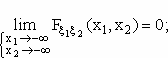
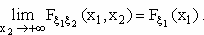
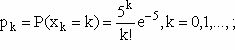
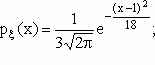
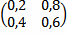 , её граф имеет вид
, её граф имеет вид 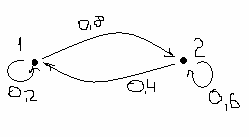 … верно
… верно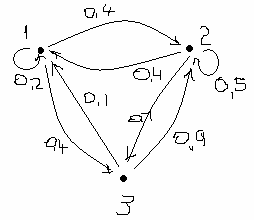 … верно
… верно Установите соотвествие
Установите соотвествие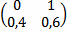 за один шаг, тогда матрица переходов за два шага имеет вид
за один шаг, тогда матрица переходов за два шага имеет вид 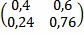 … верно
… верно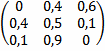 Состояние S1 означает, что процентная ставка равна 10, состояние S2 означает, что процентная ставка равна 15, состояние S3 означает, что процентная ставка равна 20. Шаг процесса - один месяц. Если сегодня процентная ставка равна 20, то через месяц матожидание будет равно… 14,5
Состояние S1 означает, что процентная ставка равна 10, состояние S2 означает, что процентная ставка равна 15, состояние S3 означает, что процентная ставка равна 20. Шаг процесса - один месяц. Если сегодня процентная ставка равна 20, то через месяц матожидание будет равно… 14,5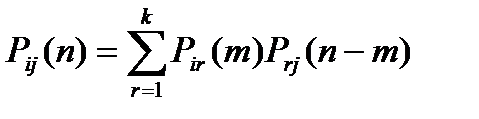

 zy
zy 
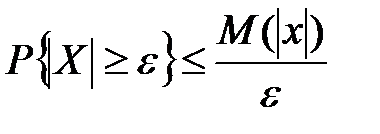
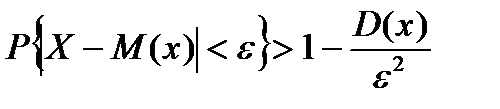 называемое… вторым неравенством Чебышева в центрированной форме
называемое… вторым неравенством Чебышева в центрированной форме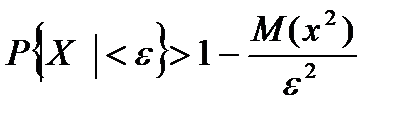 называемое… вторым неравенством Чебышева в нентрированной форме
называемое… вторым неравенством Чебышева в нентрированной форме [0;6]}, A={x; x= 1]}. P(A)=
[0;6]}, A={x; x= 1]}. P(A)= 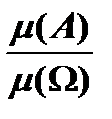 =0/6=0
=0/6=0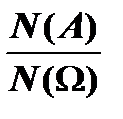 =2/6=1/3.
=2/6=1/3.