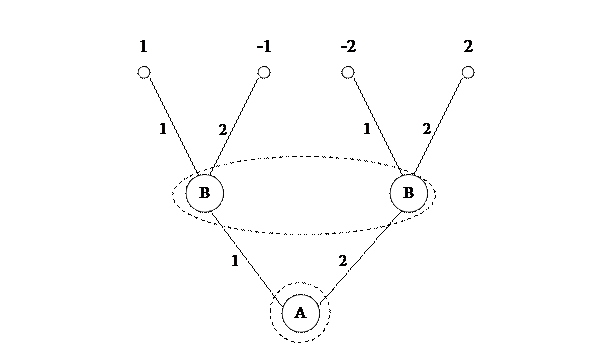
Игра с полной информацией.

1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.

2-й ход. Игрок В выбирает число у из множества двух числе {1, 2}, зная выбор числа х игроком А.

Функция W(x, y) выплат игроку А за счет игрока В задается так:

W(1,1)=1, W (2,1)=–2,

W(1,2)=–1, W(2,2)=2

На рис.1 показаны дерево игры и информационные множества.

Рис. 1. Дерево игры и информационные множества игры с полной информацией

Опишем стратегии игроков. Стратегию игрока А можно задать числом х, показывающим, какую альтернативу, первую или вторую, выбрал этот игрок. Тем самым, у игрока А две чистых стратегии:

А₁ – выбрать х=1, А₂ – выбрать х=2.

Стратегию игрока В, приняв во внимание, что выбор игрока А на 1-м ходе ему известен, удобно описать парой

[y₁, y₂].

Здесь у₁ (у₁=1,2) – альтернатива, выбираемая игроком В при условии, что игрок А выбрал первую альтернативу, х=1, а у₂ (у₂=1,2) – альтернатива, выбираемая игроком В при условии, что игрок А выбрал вторую альтернативу, х=2.

Например, выбор игроком В стратегии [2,1] означает, что если на 1-м ходе игрок А выбрал х=1, то игрок В на своем ходе должен выбрать у=2. если же на 1-м ходе игрок А выбрал х=2, то согласно этой стратегии игрок В на своем ходе должен выбрать у=1.

Таким образом, у игрока В четыре чистых стратегии:

В₁ – [1,1], y=1 при любом выборе x;

B₂ – [1,2], y=x при любом выборе x;

B₃ – [2,1], y≠x при любом выборе x;

B₄ – [2,2], y=2 при любом выборе x;

Рассчитаем выигрыши игрока А.

Пусть, например, игрок А выбрал стратегию А₁ – (1), а игрок В – стратегию В₂ – [1,2]. Тогда х=1, а из стратегии [1,2] вытекает, что у=1. Отсюда

W(x,y)=W(1,1)=1

Подобным образом рассчитываются и остальные выигрыши игрока А.

Результаты можно записать обычным образом или в виде таблицы выигрышей игрока А

		В1	В2	В3	В4
		[1,1]	[1,2]	[2,1]	[2,2]
А1	x =1	W(1,1)	W(1,1)	W(1,2)	W(1,2)
А2	x =2	W(2,1)	W(2,2)	W(2,1)	W(2,2)

или

		В1	В2	В3	В4
		[1,1]	[1,2]	[2,1]	[2,2]
А1	x =1			-1	-1
А2	x =2	-2		-2

Нетрудно заметить, что полученная матрица имеет седловую точку. Оптимальные стратегии игроков: А₁ – (1), и В₃ – [2,1]. Тем самым, игрок А на 1-м ходе выбирает х =1, а игрок В на 2-м ходу выбирает у =2. Цена игры v = –1

Игра с неполной информацией.

В данном случае на 2-м ходу игрок В выбирает число у из множества двух чисел {1,2}, не зная выбора числа х игроком А. В этом случае информационные множества выглядят так, как показано на рис. 2

Рис 2. Дерево игры и информационные множества игры с неполной информацией

Стратегии игрока А остаются прежними:

А ₁ – выбрать х = 1, А ₂ – выбрать х = 2.

Так как игроку В выбор игрока А неизвестен, т.е. игрок В не знает, в какой именно из двух позиций он находится (см. рис. 2), то у него те же две стратегии:

В ₁ – выбрать у = 1, В ₂ – выбрать у = 2.

Соответствующие таблица выигрышей игрока А и матрица игры имеют следующий вид:

 

		В 1	В 2
		у	у
А 1	х	W (1,1)	W (1,2)
А 2	х	W (2,1)	W (2,2)

или

		В 1	В 2
		у	у
А 1	х		-1
А 2	х	-2

Поученная матрица седловой точки не имеет. Оптимальные смешанные стратегии игроков: P={2/3, 1/3} и Q={½, ½}. Цена игры v = 0.