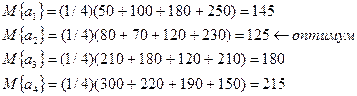Задача №7. Турфирма подбирает место для строительства летнего лагеря в Сибирской тайге для экстремального туризма в условиях дикой природы
Турфирма подбирает место для строительства летнего лагеря в Сибирской тайге для экстремального туризма в условиях дикой природы. Турфирма считает, что число туристов может быть 200, 250, 300 или 350 человек. Стоимость лагеря будет минимальной, поскольку он строится для удовлетворения только небольших потребностей. Отклонения в сторону уменьшения или увеличения относительно идеальных уровней потребностей влекут за собой дополнительные затраты, обусловленные строительством избыточных (неиспользуемых) мощностей или потерей возможности получить прибыль в случае, когда некоторые потребности не удовлетворяются. Пусть переменные а1 – а4 представляют возможные размеры лагеря (на 200, 250, 300 или 350 человек), а переменные s1 – s4 – соответствующее число участников сбора. Следующая таблица содержит матрицу стоимостей (в тыс. руб.), относящуюся к описанной ситуации.
Описанная ситуация анализируется с точки зрения следующих критериев. Критерий Лапласа. При заданных вероятностях
Минимаксный критерий. Этот критерий использует исходную матрицу стоимостей.
Критерий Сэвиджа. Матрица потерь определяется посредством вычитания чисел 50, 70, 120 и 150 из элементов столбцов от первого до четвертого соответственно. Следовательно,
Критерий Гурвица. Результаты вычислений содержатся в следующей таблице.
Используя подходящее значение для k, можно определить оптимальную альтернативу. Например, для k=0,5 оптимальным является альтернатива либо а1, либо а2, тогда как для k=0,25 оптимальным является решение а3.
|

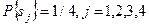 , ожидаемые значения затрат для различных возможных решений вычисляются следующим образом.
, ожидаемые значения затрат для различных возможных решений вычисляются следующим образом.