Описание алгоритма нахождения максимального потока
Изначально величине потока присваивается значение 0: f (u, v) = 0 для всех Дан граф G (V, E) с пропускной способностью c (u, v) и потоком f (u, v) = 0 для ребер из u в v. Необходимо найти максимальный поток из источника s в сток t. На каждом шаге алгоритма действуют те же условия, что и для всех потоков: · · · Остаточная сеть Gf (V, Ef) — сеть с пропускной способностью cf (u, v) = c (u, v) − f (u, v) и без потока. Вход Граф G с пропускной способностью c, источник s и сток t 1. 2. Пока есть путь P из s в t в Gf, такой что 1. Найти 2. Для каждого ребра 1. 2.
Задача №4 Найти критический путь для данного проекта
Задача №5. Менеджер – координатор аудиторской фирмы должен распределить аудиторов для работы на следующий месяц. Есть заявки от 10 клиентов на 75 аудиторов. В четырех конторах фирмы работают 90 аудиторов. 15 аудиторов можно отправить на плановую учебу. Аудиторы различаются по квалификации и опыту работы. Прежде чем приступить к аудиту конкретной фирмы, они должны затратить определенное время на подготовку и консультации. Менеджер – координатор, учитывая опыт работы аудиторов каждой конторы, оценил время, необходимое в среднем аудитору каждой конторы для подготовки к аудиту конкретного клиента. Результаты приведены в таблице. Знаки вопроса в клетках таблицы означают, что аудиторы из этой конторы не имеют опыта аудита в отрасли, которой занимается клиент, и их нельзя посылать к нему. Распределить аудиторов так, чтобы суммарные временные затраты на подготовку были минимальны.
В реальной практике обычно требуют, чтобы аудиторы не все были из одной конторы. Попробуйте выполнить это условие и не слишком ухудшить решение.
|

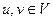 . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь. . Поток из u в v не превосходит пропускной способности.
. Поток из u в v не превосходит пропускной способности.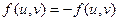 .
. для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.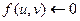 для всех ребер
для всех ребер 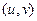
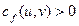 для всех ребер
для всех ребер  :
:





