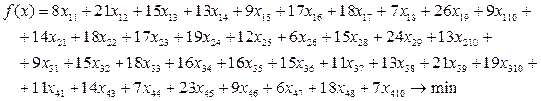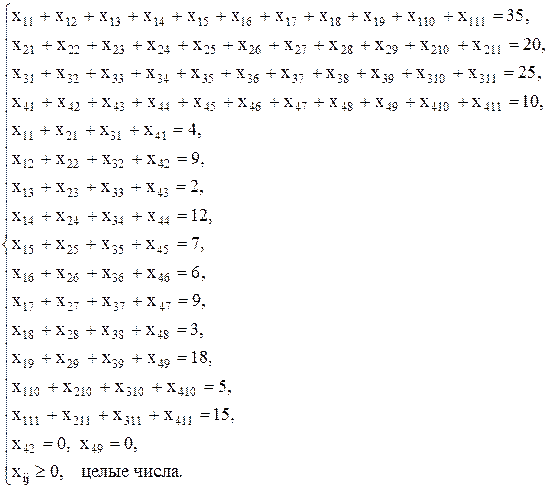Решение задачи. Обозначим через xij – число аудиторов конторы Аi, направленные на работу к клиенту Kj.
Обозначим через xij – число аудиторов конторы Аi, направленные на работу к клиенту Kj. Целевая функция, отражающая временные затраты имеет вид:
Ограничения, связанные с количеством аудиторов в фирмах и количеством заявок от клиентов, имеют вид:
Поскольку число заявок и число аудиторов в фирмах не совпадают, то введем искусственного клиента, число заявок которого равно 15 и временные затраты на работу равны 0. Система ограничений примет следующий вид:
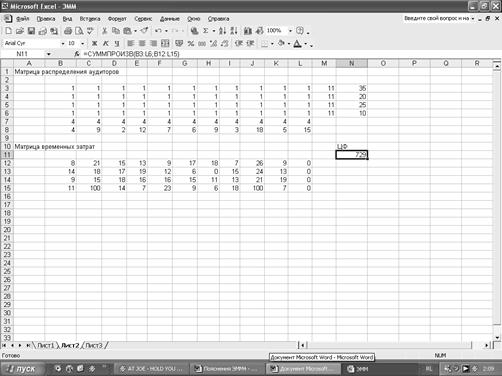
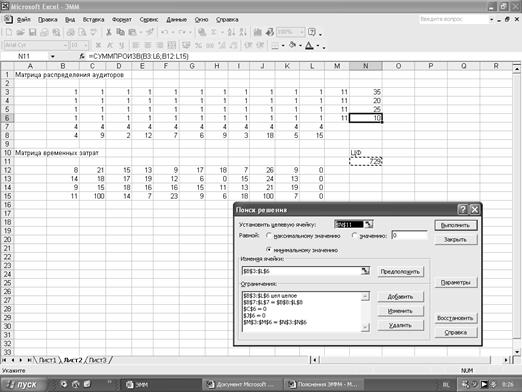
Решение задачи найдем с помощью табличного процессора MS Excel. Сформируем матрицу закрепления аудиторов за клиентами. Для этого в блок ячеек B3:L6 вводим «1». В ячейках M3:M6 суммируем по строкам. Число, имеющихся в наличии аудиторов, введем в ячейки N3:N6. В ячейках B7:L7 суммируем по столбцам. Число заявок, поданных клиентами, введем в ячейки B8:L8. Создаем матрицу временных затрат. Для этого в блок ячеек B12:L15 вводим коэффициенты целевой функции. Ячейкой целевой функции выберем N11. Поместим в ней курсор, с помощью Мастера функций выберем Категорию Математические и оттуда введем СУММПРОИЗВ, в окне СУММПРОИЗВ указываем адреса массивов B3:L6 и B12:L15. Решение задачи найдем с помощью надстройки Поиск решения. Поместим курсор в поле Установить целевую (ячейку), введем адрес $N$11, установим направление изменения целевой функции, равное Минимальному значению, введем адреса изменяемых ячеек $B$3:$L$6. Добавим ограничения: введем адреса $M$3:$M$6=$N$3:$N$6, тем самым мы реализуем условие использования всех, имеющихся в наличии аудиторов. Далее добавляем условие выполнения всех заявок: выбираем Добавить ограничение, введем адреса $B$7:$L$7=$B$8:$L$8, Затем вводим условие целочисленности изменяемых ячеек: выбираем Добавить ограничение, введем адреса $B$3:$L$6= целое. Теперь добавляем условие, что аудиторы фирмы А 4 не могут работать на клиентов К2 и К9. Используя Параметры, введем условия неотрицательности переменных и линейную модель. После введения всех ограничений, нажимаем Выполнить, на экране появляется диалоговое окно Результаты поиска решения. Получен оптимальный план распределения аудиторов, он означает следующее: у клиента К1 работают 4 аудитора фирмы А1, у клиента К2 – 2 аудитора фирмы А2 и 7 аудиторов фирмы А3, у клиента К3 – 2 аудитора фирмы А1, у клиента К4 – 2 аудитора фирмы А1 и 10 аудиторов фирмы А4, у клиента К5 – 7 аудиторов фирмы А1, у клиента К6 – 6 аудиторов фирмы А2, у клиента К7 – 9 аудиторов фирмы А2, у клиента К8 – 3 аудитора фирмы А1, у клиента К9 – 18 аудиторов фирмы А3, у клиента К10 – 5 аудиторов фирмы А1, 12 аудиторов фирмы А1 и 3 аудитора фирмы А2 отправляются на плановую учебу. При этом временные затраты составят 842 ед. В качестве примера выполнения условия о том, чтобы не все аудиторы были из одной фирмы можно привести следующее распределение аудиторов: у клиента К1 работают 3 аудитора фирмы А1 и 1 аудитор фирмы А3, у клиента К2 – 2 аудитора фирмы А2 и 7 аудиторов фирмы А3, у клиента К3 – 1 аудитор фирмы А1 и 1 аудитор фирмы А4, у клиента К4 – 6 аудитора фирмы А1 и 6 аудиторов фирмы А4, у клиента К5 – 6 аудиторов фирмы А1 и 1 аудитор фирмы А2, у клиента К6 – 5 аудиторов фирмы А2 и 1 аудитор фирмы А4, у клиента К7 – 8 аудиторов фирмы А2 и 1 аудитор фирмы А4, у клиента К8 – 2 аудитора фирмы А1 и 1 аудитор фирмы А3, у клиента К9 – 16 аудиторов фирмы А3 и 2 аудитора фирмы А2, у клиента К10 – 4 аудитора фирмы А1 и 1 аудитор фирмы А4,
13 аудиторов фирмы А1 и 2 аудитора фирмы А2 отправляются на плановую учебу. При этом временные затраты составят 888 ед.
|