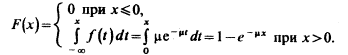Интегральная и дифференциальная функции распределения.
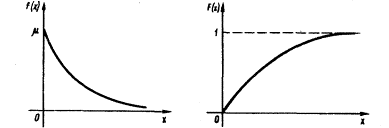
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению. Как видно из формулы, показательное распределение определяется только одним параметром m. Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения:
Графики дифференциальной и интегральной функций показательного распределения имеют вид:
|
Определение: Непрерывная случайная величина X, функция плотности которой задается выражением
