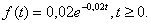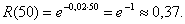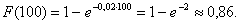Функция надежности.Пусть некоторое устройство начинает работать в момент времени t0 = 0, а по истечении времени длительностью t происходит отказ. Обозначим через Т НСВ - длительность времени безотказной работы устройства. Если устройство проработало безотказно время меньшее t, то, следовательно, за время длительностью t наступит отказ. Тогда функция распределения F(t)=P(T<t)=1- e-mt определяет вероятность отказа устройства за время t.
Функция R(t) называется функцией надежности. Выясним смысл числовых характеристик и параметра распределения.
Пример. Время безотказной работы устройства распределено по закону
Найти среднее время безотказной работы устройства, вероятность того, что устройство не откажет за среднее время безотказной работы. Найти вероятность отказа за время t= 100 часов. Решение: По условию интенсивность отказов m =0,02. Тогда среднее время между двумя отказами, т.е. математическое ожидание М(Х)=1/0,02=50часов. Вероятность безотказной работы за этот промежуток времени вычислим по функции надежности:
По функции F(t) вычислим вероятность отказа за время t =100 часов:
|
Найдем вероятность противоположного события- безотказной работы за время t: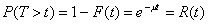
.
