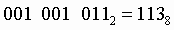Введение. Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе
Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе. Позиционные системы счисления позволяют легко производить арифметические расчёты. Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Заметьте: максимальная цифра (9) на единичку меньше количества цифр (10). Для составления машинных кодов удобно использовать не десятичную, а двоичную систему счисления, содержащую только две цифры, 0 и 1. Обратите внимание, что в двоичной системе максимальная цифра 1. Программисты для вычислений также пользуются ещё восьмеричной и шестнадцатеричной системами счисления. Количество цифр используемых в системе счисления называется её «основанием». В десятичной системе основание равно десяти, в двоичной системе - двум, ну а в восьмеричной и шестнадцатеричной - соответственно, восьми и шестнадцати. То есть в р-ичной системе счисления количество цифр равно р и используются цифры от 0 до р-1. В общем случае в позиционной системе счисления числа представляются следующим образом: (anan − 1... a 0) f, где a 0, a 1,..., an — цифры, а f — основание системы счисления. Если используется десятичная система, то f — можно опустить. Примеры чисел: § 110012 — число в двоичной системе счисления, a 0 = 1, a 1 = 0, a 2 = 0, a 3 = 1, a 4 = 1; § 2213 — число в троичной системе счисления, a 0 = 1, a 1 = 2, a 2 = 2; § 318 — число в восьмеричной системе счисления, a 0 = 1, a 1 = 3; § 2510 — число в десятичной системе счисления, a 0 = 5, a 1 = 2;
12.2Правила перевода чисел из одной системы счисления в другую Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода. 1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней двойки: Таблица 4. Степени числа 2
Пример. Число 2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней восьмерки: Таблица 5. Степени числа 8
Пример. Число 3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней числа 16: Таблица 6. Степени числа 16
Пример. Число Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке. Пример. Число
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример. Число
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример. Число
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3). Пример. Число
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
|

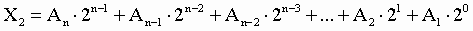
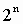
 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

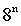
 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
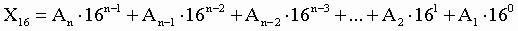

 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
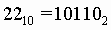
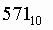 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.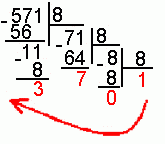
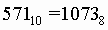
 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.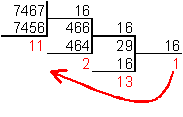
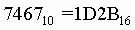
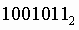 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.