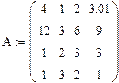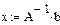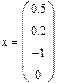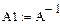Погрешность решения и обусловленность системы уравнений
Рассмотрим влияние погрешности правой части и свойств матрицы системы линейных уравнений на погрешность решения. Пусть правая часть системы задана приближенно, с погрешностью η:
A x = b 1, b 1 = b + η.
Пусть x 1 решение неточно заданной системы A x = b 1, а x решение точной системы A x = b. Обозначим погрешность решения через r = x 1 – x. Тогда можно записать A x 1= b 1 в виде A (x + r)= b + η, и A r = η. Определение 3.3. Мерой обусловленности системы называется число
Мера обусловленности системы равна верхней грани отношения относительной погрешности решения к относительной погрешности правой части. Из формулы (3.29) следует неравенство
Если мера обусловленности системы принимает большое значение, то это означает, что небольшая погрешность правой части может привести к большой погрешности решения, т.е. полученное приближенное решение окажется непригодным. Учитывая, что r = A –1η, можно получить формулу вычисления меры обусловленности системы:
Определение 3.4. Мерой обусловленности матрицы A называется число
Для вычисления меры обусловленности матрицы можно с помощью (3.31) получить формулу
Учитывая (3.30), можно записать
Неравенство (3.34) связывает относительные погрешности правой части и решения системы через свойства матрицы системы. Определение 3.5. Системы уравнений и матрицы называются плохо обусловленными, если их меры обусловленности принимают большие значения, и хорошо обусловленными, если их меры обусловленности принимают малые значения. Понятно, что при решении хорошо обусловленных систем малые погрешности правой части приводят к малым погрешностям решения, а плохо обусловленные системы уже нельзя решать обычными методами. Пример 3.7. Для данной системы линейных уравнений исследовать влияние погрешности правой части на погрешность решения.
Решение. Решение системы x = (0,5; 0,2; –1; 0) T можно найти в программе Mathcad по формуле x = A –1∙ b, где A — матрица коэффициентов, а b — вектор правых частей:
Если мы изменим правые части на 0,01 (прибавим к каждой координате вектора b число 0,01), то получим приближенное решение x 1 = (0,342; 0,634; –1,9; 0,667) T, которое отличается от точного решения на вектор x 1 – x =
Мы видим, что незначительные погрешности правой части приводят к решению, которое сильно отличается от точного. Это объясняется плохой обусловленностью матрицы системы. Действительно, если мы вычислим число обусловленности матрицы A по формуле (3.33), пользуясь определением нормы (3.19), используя функцию программы Mathcad eigenvals(A T∙ A), получим:
Отсюда получим значение числа обусловленности матрицы A:
|| A || = 322,2650,5 = 17,95, || A –1|| = 367200,5 = 191,62, τ = || A ||∙|| A –1|| = 3439,7.
|

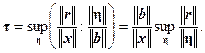 (3.29)
(3.29) (3.30)
(3.30) (3.31)
(3.31)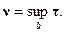 (3.32)
(3.32)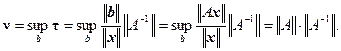 (3.33)
(3.33)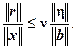 (3.34)
(3.34)