Метод Гаусса для решения систем линейных уравнений
Пусть требуется решить систему n линейных алгебраических уравнений с n неизвестными:
Прямой ход метода Гаусса преобразует систему (3.9) к треугольному виду исключением соответствующих неизвестных. Пусть a 11 ≠ 0. Первый шаг заключается в исключении переменной x 1 с помощью первого уравнения из остальных уравнений. Разделим первое уравнение на a 11:
Затем от второго уравнения отнимем первое уравнение, умноженное на a 21. В результате, на месте второго уравнения получим уравнение, не содержащее x 1. Чтобы исключить x 1 из третьего уравнения отнимем от него первое уравнение, умноженное на a 31. Аналогично исключаем x 1 из четвертого и последующих уравнений. Для исключения x 1 из i -го уравнения (i = 2, 3, …, n) применим формулы:
В результате этих вычислений получим систему вида:
На втором шаге исключаем переменную x 2 с помощью второго уравнения из третьего и последующих уравнений. Предположим, что
В системе (3.12) с помощью второй строки исключим x 2 из i -го уравнения(i = 3, 4, …, n), применяя формулы:
Система (3.12) преобразуется к следующему виду:
1. В общем случае, на шаге m, для m = 1, 2, …, n – 1, делим сначала m -ое уравнение на
а затем исключаем переменную xm с помощью m -ого уравнения из i -го,
Здесь предполагается, что на каждом шаге выполняется условие В результате (n – 1)-го шага система (3.9) приобретает вид:
2. Обратный ход метода Гаусса вычисляет неизвестные xi в обратном порядке. Из последнего уравнения в (3.18) находим
Неизвестные xi определяем по следующим формулам:
Метод Гаусса предполагает, что на m -ом шаге выполняется условие Чтобы избежать этих трудностей применяют метод Гаусса с выбором главного элемента. В качестве ведущего элемента на каждом шаге выбирают наибольший по модулю элемент столбца и переставляют соответствующую строку с другой строкой так, чтобы найденный элемент стал диагональным, затем исключают соответствующую переменную. Так как при этих перестановках в уравнениях переменные остаются на своих местах, решение преобразованной системы совпадает с решением исходной системы уравнений. Метод Гаусса с выбором главного элемента по столбцам отличается от алгоритма (3.16) — (3.20) только тем, что перед преобразованием (3.16) надо выполнить поиск максимального по модулю элемента в m -ом столбце и переставить строки системы уравнений так, чтобы максимальный элемент стал диагональным элементом матрицы коэффициентов.
|

 (3.9)
(3.9)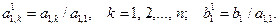 (3.10)
(3.10)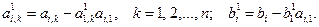 (3.11)
(3.11)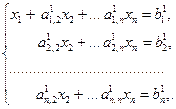 (3.12)
(3.12)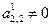 . Разделим второе уравнение на
. Разделим второе уравнение на 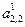 :
: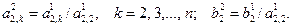 (3.13)
(3.13) (3.14)
(3.14)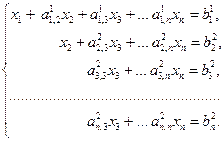 (3.15)
(3.15) :
: (3.16)
(3.16) (3.17)
(3.17) .
.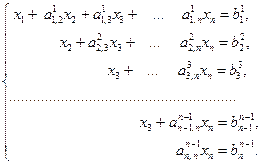 (3.18)
(3.18)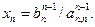 (3.19)
(3.19) (3.20)
(3.20) близок к нулю, что тоже может привести к неприятностям в виде больших погрешностей.
близок к нулю, что тоже может привести к неприятностям в виде больших погрешностей.


