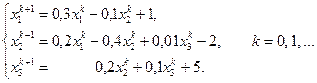Итерационный метод
Запишем систему уравнений (3.9) в виде
A x = b, (3.21) где A — матрица коэффициентов, а b — вектор правых частей системы. Преобразуем (3.21) к виду, удобному для итераций x = B x + c. (3.22)
Тогда метод простой итерации определяется формулой: x k +1 = B x k + c, k = 0, 1, … (3.23)
где начальное приближение x 0 задано. Сформулируем теоремы об условиях сходимости метода простых итераций (доказательство теорем приведено в [1]). Теорема 3.1 (достаточное условие сходимости).Если || B || < 1, то система (3.21) имеет единственное решение, а итерационный метод (3.23) сходится к решению со скоростью геометрической прогрессии. Теорема 3.2 (необходимое и достаточное условие сходимости).Пусть система (3.22) имеет единственное решение. Итерационный процесс (3.23) сходится к решению системы (3.22) тогда и только тогда, когда все собственные значения матрицы B по модулю меньше единицы. Теоремы 3.1 и 3.2 не дают способов преобразования произвольной системы линейных уравнений к виду (3.22) так, чтобы метод итераций (3.23) при этом сходился к решению. Эти теоремы имеют важное теоретическое значение. Отметим, что на практике для проверки условия сходимости метода итераций более полезна теорема 3.1, а теорему 3.2 удается использовать тогда, когда собственные значения матрицы B известны. Задача определения собственных значений матрицы в общем случае сложнее, чем решение системы линейных уравнений. Для преобразования системы уравнений к виду, удобному для итераций можно [7] умножить систему (3.21) на матрицу D = A –1 – ε, где ε — произвольная матрица. Тогда система примет вид (3.22)
x = B x + c, B = ε A, c = D b (3.24)
и матрица B будет удовлетворять теореме (3.1), если выбрать элементы матрицы ε достаточно малыми по модулю. Однако, этот прием не выгоден, так как для вычисления обратной матрицы A –1 необходимо выполнить не меньше операций, чем на решение самой системы. При небольшом числе уравнений систему иногда удается привести к виду, удобному для итераций с помощью нескольких преобразований. Пример, иллюстрирующий этот способ, содержится в [7]. Ниже, в последующих главах, будут рассмотрены разностные методы решения краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных, которые приводят к решению систем линейных уравнений с большим числом неизвестных. Учитывая специфику таких систем, часто удается построить эффективные итерационные методы решения. Пример 3.4. Система линейных уравнений приведена к виду, удобному для итераций. Проверить условия сходимости и найти решения.
Решение. Найдем норму матрицы B и проверим условие сходимости
По теореме 3.1 мы имеем сходящийся итерационный процесс:
Выберем в качестве начального приближения вектор свободных членов x 0 = (1, –2, 5) T и проведем вычисления в программе Excel. 1) В ячейки A 2: C 4 введем элементы матрицы B, а в ячейки F 2: F 4 — свободные члены, как показано в таблице 3.3. 2) В столбце D будем вычислять последовательные приближения к решению. В ячейках D 2: D 4 запишем начальное приближение, т.е. введем числовые значения компонент вектора x 0: 1, –2, 5. Выделим диапазон D 5: D 7, введем формулу =МУМНОЖ(A$2:C$4;D2:D4)+F$2:F$4 и, удерживая нажатыми клавиши Ctrl и Shift, нажмем Enter. В ячейках D 5: D 7 появятся значения компонент вектора x 1. Выделим D 5: D 7 и с помощью мыши протянем маркер заполнения вниз до D 22. Здесь надо иметь ввиду, что в ячейках D 5: D 7 записана операция с массивом, поэтому число новых строк, в которые копируем эти ячейки, должно быть кратно 3. В нашем случае имеем 15 строк, т.е. 5 новых итераций, а всего, с учетом D 5: D 7, выполнено 6 итераций. 3) В столбце E вычислим разности между компонентами последовательных приближений x k и x k +1. Выделим диапазон E 5: E 7, введем формулу =ABS(D2:D4-D5:D7), и протянем маркер заполнения вниз до E 22. В ячейках
x 1 ≈ 1,59; x 2 ≈ – 1,16; x 3 ≈ 5,29.
В табл. 3.3 показано содержимое ячеек A 1: F 7 в режиме формул, которое высвечивается, если выполнить команду меню «Сервис — параметры», выбрать вкладку «Вид» и отметить в параметрах окна флажком пункт «формулы». Если этот флажок снять, то увидим вычисленные компоненты решения. Таблица 3.3
Составим программу на языке C ++ для решения системы уравнений методом итераций:
#include <except.h> #include <iostream.h> #include <math.h> int iter(long double **b, long double *c, long double *x, long double eps, int k_max, const int n); int main(){ long double **b; long double *c, *x, eps; int i,j,n,k_max; cout <<"\n input n = "; cin >> n; cout <<"\n input eps = "; cin >> eps; cout <<"\n input k_max = "; cin >> k_max; try { b= new long double*[n]; for(i=0;i<n;i++) b[i]=new long double[n]; c= new long double[n]; x= new long double[n]; } catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} cout <<"\n input matrix b \n"; for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> b[i][j]; cout <<"\n input vector c\n"; for (i=0; i<n; i++)cin >> c[i]; cout << "\n matrix b: "; for (i=0; i<n; i++){cout << "\n"; for (j=0; j<n; j++) cout <<" "<< b[i][j];} cout << "\n vector c: "; for (i=0; i<n; i++)cout << "\n " << c[i]; iter(b, c, x,eps,k_max, n); cout << "\n vector x: "; for (i=0; i<n; i++)cout << "\n x[" << i <<"] = " << x[i]; cout << "\n Press Key and Enter to continue"; cin >> i; // for pause for(i=0;i<n;i++)delete[] b[i]; delete b; delete[] c; delete[] x; return 0; }//end main int iter(long double **b, long double *c, long double *x, long double eps, int k_max, const int n){ int i, j, m; long double *x1, xerr; try {x1 = new long double[n];} catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} for (m = 0; m <= k_max; m++) {// m for (i = 0; i < n; i++){ x1[i] = c[i]; for (j = 0; j < n; j++) x1[i] = x1[i] + b[i][j]*x[j];} xerr = 0; for (i = 0; i < n; i++) xerr = xerr + (x1[i] - x[i])* (x1[i] - x[i]); xerr = sqrt(xerr); for (i = 0; i < n; i++) x[i] = x1[i]; if(xerr < eps) break; }// end m delete[] x1; return 0; }// end iter
Найдем с помощью этой программы решение системы уравнений примера 3.4:
input n = 3 input eps = 0.00001 input k_max = 10000 input matrix b 0.3 –0.1 0 0.2 –0.4 0.01 0 0.2 0.1 Input vector c 1 –2 5 matrix b: 0.3 –0.1 0 0.2 –0.4 0.01 0 0.2 0.1 vector c: –2 vector x: x[0] = 1.5947 x[1] = –1.16292 x[2] = 5.29713 Press Key and Enter to continue
Как видим, решение совпадает с решением, полученным в программе Excel.
|


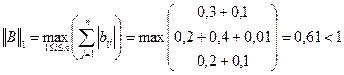 .
.