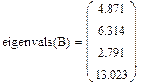Вычисление всех собственных значений положительно определенной симметричной матрицы
Приведем алгоритм для вычисления нескольких первых или всех собственных значений и соответствующих собственных векторов положительно определенной симметричной матрицы. Пусть уже вычислены первые m собственных значений λ1, λ2, …, λ m и m соответствующих собственных векторов x 1, x 2, …, x m. Алгоритм вычисления очередного (m + 1)-го собственного значения и соответствующего собственного вектора. 0. Выберем начальное приближение 1. Вычисляем k -е приближение к собственному значению λ m +1:
2. Находим вектор
3. Если m > 0 ортогонализируем вектор
4. Нормируем полученный вектор
5. k = k + 1; Процесс 1. —5. повторяется до тех пор, пока не будет выполнено условие сходимости итераций
где ε – заданная погрешность.
При вычислении первого собственного значения и соответствующего вектора пункт 3) пропускается. Этим алгоритмом можно вычислить все собственные значения и собственные векторы. Пример 3.11. Найти все собственные значения и соответствующие собственные векторы матриц:
1) Решение с помощью программы на языке C ++. Реализуем алгоритм (3.42) — (3.46) на языке C ++ и проверим программу на данном примере, сравнивая полученный результат с ответами из примеров 3.9, 3.10. Текст программы приведен ниже:
#include <iostream.h> #include <except.h> #include <stdlib.h> #include <math.h> int Eigen(long double **a, long double **x, long double *eigv, long double eps, const int n, int k_max); long double s_prod(long double *x1, long double *x2, const int n); int gauss(long double **a, long double *b, long double *x, const int n); int main(){ long double **a, **x, *eigv, eps; int i,j,n,k_max; cout <<"\n input n = "; cin >> n; cout <<"\n input k_max = "; cin >> k_max; cout <<"\n input eps = "; cin >> eps; try { a = new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n]; x = new long double*[n]; for(i=0;i<n;i++) x[i]=new long double[n]; eigv = new long double[n]; } catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} cout <<"\n input matrix a: \n"; for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j]; cout <<"\n matrix a:"; for (i=0; i<n; i++){ cout << "\n ";for (j=0; j<n; j++)cout <<" "<< a[i][j];} Eigen(a, x, eigv, eps, n, k_max); for(i = 0; i < n; i++)cout << "\n Eigen Value [" << i << "] = " << eigv[i]; cout << "\n Eigen Vectors: "; for (i=0; i<n; i++){ cout <<"\n "; for (j=0; j<n; j++) cout << " " << x[i][j];} cout <<"\n "; cin >> i; // for pause for(i = 0; i < n; i++) delete[] a[i]; delete a; for(i = 0; i < n; i++) delete[] x[i]; delete x; delete[] eigv; return 0; }//end main -------------------------------------------------------------- int Eigen(long double **a, long double **x, long double *eigv, long double eps, const int n, int k_max){ int i, j, k, m; long double **a1,*x0,*x1,*alf, xerr, xnrm, eig0, eig1,s; a1 = new long double*[n]; for(i=0;i<n;i++) a1[i]=new long double[n]; x0 = new long double[n]; x1 = new long double[n]; alf = new long double[n]; for(m = 0; m < n; m++){ // 0. k = 0; for(i = 0; i < n; i++)x0[i] = 1.; eig0 = 0; do { // 1. for(i = 0; i < n; i++){s = 0; for(j = 0; j < n; j++)s += a[i][j]*x0[j]; x1[i] = s;} eig1 = s_prod(x1,x0,n)/s_prod(x0,x0,n); // 2. for(i = 0; i < n; i++)x1[i] = eig1*x0[i]; for(i = 0; i < n; i++) for(j = 0; j < n; j++)a1[i][j] = a[i][j]; gauss(a1,x1,x0,n); // 3. if(m > 0){ for(j = 0; j < m; j++){ for(i = 0; i < n; i++)x1[i] = x[i][j]; alf[j] = s_prod(x0,x1,n)/s_prod(x1,x1,n); } for(i = 0; i < n; i++) for(j = 0; j < m; j++)x0[i]= x0[i] - x[i][j]*alf[j]; }// end if // 4. xnrm = sqrt(s_prod(x0,x0,n)); for(i = 0; i < n; i++)x0[i] = x0[i] / xnrm; xerr = fabs(eig1 - eig0); eig0 = eig1; k = k + 1; if (k > k_max)break; }while (xerr > eps); eigv[m] = eig1; for(i = 0; i < n; i++) x[i][m] = x0[i]; }// end m for(i = 0; i < n; i++) delete[] a1[i]; delete a1; delete[] x0; delete[] x1; delete[] alf; return 0; }// end Eigen
long double s_prod(long double *x1, long double *x2, const int n){ long double s; int i; s = 0; for(i = 0; i < n; i++)s = s + x1[i]*x2[i]; return s; }// end s_prod
int gauss(long double **a, long double *b, long double *x, const int n){ int i, k, m; long double amm, aim; for (m = 0; m <= n-2; m++) {// m amm = a[m][m]; for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm; // 3.16 b[m] = b[m] / amm; // for (i = m + 1; i <= n-1; i++){// i aim = a[i][m]; for (k = m; k <= n-1; k++) a[i][k] = a[i][k] - a[m][k]*aim; // 3.17 b[i] = b[i] - b[m]*aim; // }// end i }// end m x[n-1] = b[n-1]/a[n-1][n-1]; // 3.19 for (i = n - 2; i >= 0; i--){// i x[i] = b[i]; // for (k = i + 1; k < n; k++) // 3.20 x[i] = x[i] - a[i][k]*x[k]; // }// end i return 0; }// end gauss
Приведем результаты расчетов: 1) Для матрицы A:
Input n = 3 Input k_max = 100 Input eps = 0.001 Input matrix a: 3 1 0 1 2 0 0 0 2 matrix a: 3 1 0 1 2 0 0 0 2 Eigen Value [0] = 1.38279 Eigen Value [1] = 1.99985 Eigen Value [2] = 3.61796 Eigen Vectors: -0.525551 0.0189405 0.850551 0.850389 -0.0179017 0.52585 0.0251862 0.99966 -0.00669857
2) Для матрицы B:
Input n = 4 Input k_max = 1000 Input eps = 0.0000001 Input matrix a: 5 -1 0 0 -1 7 4 1 0 4 8 3 0 1 3 7 matrix a: 5 -1 0 0 -1 7 4 1 0 4 8 3 0 1 3 7 Eigen Value [0] = 2.79088 Eigen Value [1] = 4.87123 Eigen Value [2] = 6.31445 Eigen Value [3] = 13.0234 Eigen Vectors: 0.279353 0.861671 0.41803 -0.0688165 0.617008 0.110771 -0.549768 0.552074 -0.660456 0.261569 0.018022 0.703602 0.324131 -0.420517 0.722967 0.442067
Приведем для дополнительной проверки правильности работы программы результаты расчета собственных значений и собственных векторов я матрицы B в программе Mathcad:
Сравнив эти результаты, можно сделать вывод о корректности работы программы и правильности алгоритма (3.42) — (3.46). Замечание. Так как программа носит учебный характер, интерфейс программы сделан простым, достаточным на наш взгляд для понимания алгоритма. В частности, если размерность матрицы больше четырех, то вывод матрицы на экран может быть не таким наглядным (строка матрицы может не поместиться в одну строку экрана). В этом случае студентам предлагается изменить программу в соответствующей части.
|

 ; k = 0;
; k = 0; ; (3.42)
; (3.42) из уравнения
из уравнения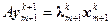 ; (3.43)
; (3.43) к первым m собственным векторам
к первым m собственным векторам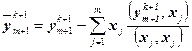 (3.44)
(3.44)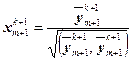 (3.45)
(3.45) , (3.46)
, (3.46)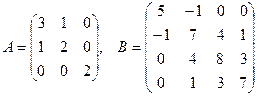 .
.