Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.
1. Зададим начальное приближение x 0 к собственному вектору; k = 0; 2. Вычисляем следующие приближения x k +1 формулам
3. Если |λ k +1 – λ k | ≥ ε, переходим к пункту 2, иначе — к 4; 4. Конец.
Критерием для остановки итераций является условие |λ k +1 – λ k | < ε, где ε — заданная погрешность. В (3.40) можно вычислить сначала k -ю степень матрицы A и умножить её на вектор x 0 (см. пример 3.10), а в формуле для λ k можно брать отношение ненулевой координаты вектора x k +1 к соответствующей координате вектора x k, которая тоже не должна быть равной нулю. Так как заранее не известно, какие координаты собственного вектора не равны нулю, то лучше брать отношение сумм координат. Пример 3.10. Найти наибольшее по модулю собственное значение и соответствующий собственный вектор матрицы A из примера 3.9. Решение. Проведем расчеты в программе Mathcad. Вычислим
Полученные результаты практически совпадают с решением предыдущего примера 3.9. Составим на C ++ программу вычисления наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы A по формулам (3.40):
#include <iostream.h> #include <except.h> #include <math.h> int EigenMax(long double **a, long double *eig_val,long double *x0, long double *x1, long double eps, const int n, int k_max); int main(){ long double **a, *x0, *x1, eigv, eps; int i,j,n,k_max; cout <<"\n input n = "; cin >> n; cout <<"\n input k_max = "; cin >> k_max; cout <<"\n input eps = "; cin >> eps; try { a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n]; x0= new long double[n]; x1= new long double[n]; } catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} cout <<"\n input matrix a \n"; for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j]; for (i=0; i<n; i++){cout << "\n";for (j=0; j<n; j++)cout <<" "<< a[i][j];} cout <<"\n input vector x0\n"; for (i=0; i<n; i++)cin >> x0[i]; for (i=0; i<n; i++)cout << "\n x0[" << i <<"] =" << x0[i]; eigv = 0; EigenMax(a, &eigv, x0, x1,eps, n, k_max); cout << "\n Max Eigen Value = " << eigv; cout << "\n Eigen Vector: "; for (i=0; i<n; i++)cout << "\n x1[" << i <<"] =" << x1[i]; cin >> i; // for pause for(i = 0; i < n; i++) delete[] a[i]; delete a; delete[] x0; delete[] x1; return 0; }//end main int EigenMax(long double **a, long double *eig_val,long double *x0, long double *x1, long double eps, const int n, int k_max){ int i, j, k; long double xerr, xnrm, eig0, s, s0, s1; k = 0; do { eig0 = *eig_val; for (i = 0; i < n; i++){ s = 0; for (j = 0; j < n; j++)s += a[i][j]*x0[j]; x1[i] = s;} s0 = 0; s1 = 0; for (i = 0; i < n; i++){s0 += x0[i]; s1 += x1[i];} *eig_val = s1/s0; xerr = fabs(*eig_val - eig0); xnrm = 0; for (i = 0; i <= n-1; i++) xnrm += x1[i]*x1[i]; xnrm = sqrt(xnrm); for (i = 0; i < n; i++){x1[i] = x1[i]/xnrm; x0[i] = x1[i]; } k = k + 1; if (k > k_max)break; }while (xerr > eps); return 0; }// end EigenMax
Найдем с помощью этой программы наибольшее собственное значение матрицы из примера 3.10:
Input n = 3 Input k_max = 1000 Input eps = 0.000001 Input matrix a 3 1 0 1 2 0 0 0 2 3 1 0 1 2 0 0 0 2 Input vector x0 Max Eigen Value = 3.61795 Eigen Vector: x1[0] =0.850651 x1[1] =0.525731 x1[2] =3.81633e–05
Результаты с заданной точностью совпадают со значениями, найденными в примерах 3.9, 3.10.
|

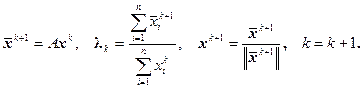 (3.40)
(3.40)



