I.  т.к.
т.к. 
 , для
, для  , то формула Маклорена имеет вид
, то формула Маклорена имеет вид 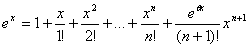 .
.
На любом отрезке  , где
, где  в силу того, что:
в силу того, что:  , т.е.
, т.е.  , получаем следующую оценку следующего члена
, получаем следующую оценку следующего члена 
Полагая здесь x=r=1 имеем оценку погрешности приближенного вычисления числа e 
II.  т.к.
т.к.  ,
, 
 то формула Маклорена имеет вид
то формула Маклорена имеет вид 
 ;
;
Здесь n – нечетное число x – в радианах.
Очевидно, что на любом отрезке 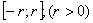 справедлива следующая оценка остаточного члена:
справедлива следующая оценка остаточного члена: 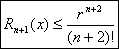
III.  Т.к.
Т.к.  ;
; 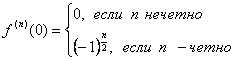 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид: 
 ;
;
Здесь n – четное число на любом отрезке 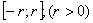 имеет очевидно для остаточного члена оценку
имеет очевидно для остаточного члена оценку
IV.  Т.к.
Т.к. 
 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид:  где остаточный член имеет вид:
где остаточный член имеет вид: 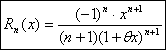 в форме Лагранжа. для значений
в форме Лагранжа. для значений 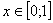 имеем оценку, переходя в к модулям:
имеем оценку, переходя в к модулям: 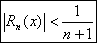 ;
;
Для значений  можно доказать, что имеет место оценка:
можно доказать, что имеет место оценка: 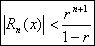
V.  , где
, где  Т.к
Т.к 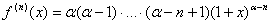
 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид: 
 ; В частности когда
; В частности когда  (натуральное число), то получаем формулу бинома Ньютона:
(натуральное число), то получаем формулу бинома Ньютона: 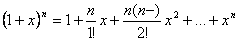 .
.

 т.к.
т.к. 
 , для
, для  , то формула Маклорена имеет вид
, то формула Маклорена имеет вид 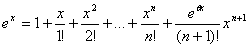 .
. , где
, где  в силу того, что:
в силу того, что:  , т.е.
, т.е.  , получаем следующую оценку следующего члена
, получаем следующую оценку следующего члена 

 т.к.
т.к.  ,
, 
 то формула Маклорена имеет вид
то формула Маклорена имеет вид 
 ;
;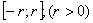 справедлива следующая оценка остаточного члена:
справедлива следующая оценка остаточного члена: 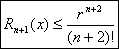
 Т.к.
Т.к.  ;
; 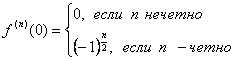 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид: 
 ;
; Т.к.
Т.к. 
 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид:  где остаточный член имеет вид:
где остаточный член имеет вид: 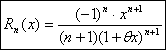 в форме Лагранжа. для значений
в форме Лагранжа. для значений 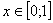 имеем оценку, переходя в к модулям:
имеем оценку, переходя в к модулям: 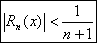 ;
; можно доказать, что имеет место оценка:
можно доказать, что имеет место оценка: 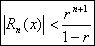
 , где
, где  Т.к
Т.к 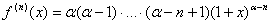
 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид: 
 ; В частности когда
; В частности когда  (натуральное число), то получаем формулу бинома Ньютона:
(натуральное число), то получаем формулу бинома Ньютона: 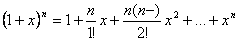 .
.


