II. Численные методы
Решение алгебраических уравнений Средство «Подбор параметра» Общие сведения Инструмент Подбор параметра являетсяодним из вычислительных средств MS Excel. С его помощью можно решать алгебраические уравнения или подбирать значения ячейки, от которой зависят значения других ячеек. При этом в зависимых ячейках должны находиться формулы, в которые исходная ячейка входит как параметр. Пример Цена на товар вначале увеличилась на 25%,а затем снизилась на 15%, после чего она стала равной 163 руб. Определить исходную цену товара. Решение. 1. Подготовим в Excel таблицу для расчета итоговой цены, считая первоначальную цену известной и равной, например, 100 р.
В итоге в ячейке B3 получим значение, равное 106,25. Чтобы подобрать исходную цену, при которой итоговая цена станет равной 163 р. выполните 2. Выберите в меню Сервис команду Подбор параметра …
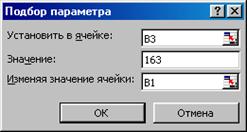
Рис.2.1. Окно Подбор параметра
В появившемся окне (рис.2.1) введите для поля Установить в ячейке значение B3, для поля Значение – 163, для поля Изменяя значение ячейки – B1. После нажатия кнопки ОК Excel автоматически подберет значение ячейки B1,при которой в B3 получится результат, равный 163. Таким значением окажется цена 151,41 р. Варианты заданий 1. Определить, какой должна быть оптовая цена товара, чтобы вместе с 16% торговой наценкой и с последующим 5% президентским налогом с продажи розничная цена равнялась 25 руб.
2. Банк ежемесячно начисляет проценты по формуле сложных процентов:
где S – текущий вклад; P – начальный вклад; c – сложная ставка; t – время. Определить, какой должна быть исходная сумма, чтобы через 6 месяцев общая сумма вклада оказалась равной 2000 руб.
3. Банк ежемесячно начисляет 5% от суммы вклада. Определить, каким должна быть исходная сумма, чтобы через 6 месяцев общая сумма вклада оказалась равной 2000 руб.
4. Спрос на товары А и В меняется соответственно по закону Sa=100+3t Sb=2et, где t – время в месяцах. Определить, в какой момент Sb станет больше, чем Sa. Указание: следует найти t такое, чтобы разность Sb - Sa оказалась равной 0.
5. При расчете отпускной цены подакцизного товара поступают следующим образом: 1) вначале учитывают норму рентабельности C1 = S * (100 + r), где S – себестоимость (руб.) r – норма рентабельности (в %) 2) находят отпускную цену по формуле:
где s – акцизная ставка (в %) Пользуясь электронными таблицами Excel, составить расчет С по данным S, r, 1) Найти С при S = 6000, r = 20%, s = 20%. 2) определить с помощью инструмента Подбор параметра, какой должна быть себестоимость S, если с= 8000(при тех же r и s).
6. Валовой доход предприятия в 2004 году составил 100000 $. В предыдущие 5 лет (начиная с 1999 г.) он изменялся следующими темпами: +10%, +20%, +15%, -30%, +20%. Определить годовой доход предприятия в 1999 г.
7. Банк ежемесячно начисляет проценты по формуле простых процентов:
где S – текущий вклад; P – начальный вклад; c – простая ставка; t – время. Определить время, через которое вклад возрастет в 2 раза.
8. Банк ежемесячно начисляет проценты по формуле простых процентов:
где S – текущий вклад; P – начальный вклад; c – простая ставка; t – время. Определить, каким должна быть исходная сумма, чтобы через 6 месяцев общая сумма вклада оказалась равной 2000 руб.
9. Наследство в 15 млрд. долларов, оставшееся после смерти миллиардера NN, необходимо на основании завещания поделить между наследниками, начиная с родственников первого уровня и заканчивая пятым уровнем родства, соблюдая следующие условия: – доли родственников одинакового уровня равны; – доли родственников первого, второго, третьего, четвертого и пятого уровня выраженные в долларах, находятся по отношению друг к другу в следующей пропорции: x5: x4: x3: x2: x; где x – некоторое положительное число, отличное от 1. Всего оказалось 3 родственника первого уровня, 8 родственников второго уровня, 20 родственников третьего уровня, 75 родственников четвертого уровня и 226 родственников пятого уровня. Определить, как следует распределить наследство.
10. Цена товара снижалась дважды: вначале на 30%, а затем еще на 10 %, после чего стала равной 120 р. Найти первоначальную цену.
11. Турист побывал в четырех странах. При этом он: – во Франции он истратил денег в 2 раза больше, чем в Германии; – в Дании в 3 три раза меньше, чем во Франции; – в Испании в 1.5 раза больше, чем в Дании. Определить сколько денег он истратил в каждой стране, если его общие расходы составили 5000$.
12. Банк ежемесячно начисляет проценты по формуле сложных процентов:
где S – текущий вклад; P – начальный вклад; c – сложная ставка; t – время. Определить, через сколько месяцев сумма вклада увеличится в 1.5 раза
13. Один банк начисляет проценты по вкладам по сложным процентам, а второй – по простым (см. задания 2, 7). При заданных значениях ставок определить через сколько месяцев стоимость вклада по сложным процентам превзойдет стоимость вклада по простым процентам.
14. Начальная цена некоторого товара была равна 100 руб. После двукратного подорожания на одно и то же количество процентов его цена стала равна 144 руб. Найти величину однократной наценки.
|

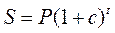 ,
,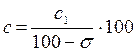 ,
, s.
s. ,
,


