Реализация расчетов в Excel
Пусть нам дана следующая система уравнений:
В матричном виде уравнение (4) выглядит следующим образом:
Процесс решения уравнения (2.4) или (2.4а) состоит в последовательном вычислении компонентов уравнения (2.3). 1) В ячейках D5:F7 разместим матрицу коэффициентов; 2) В ячейках H5:H7 разместим вектор–столбец Y;
3) Получим транспонированную матрицу AT. Для этого: – копируем ячейки D5:F7 в буфер; – устанавливаем курсор в ячейку D11; – выполняем команды Правка > Специальная вставка > Транспонировать > Ok.
4) Вычислим матрицу АТ Y. Для этого: – курсор устанавливаем ячейку D16; – вызываем функцию МУМНОЖ (из категории «Математические»); – в качестве «Массив1» указать адрес транспонированной матрицы D11:F13; – в качестве «Массив2» указать адрес матрицы Y (H5:H7); – после «Ok» в D16 появится только первый элемент массива (число 31); – для того, чтобы увидеть остальные числа: выделяем ячейки D16:D18; нажимаем F2; выполняем тройное нажатие Ctrl + Shift + Enter.
5) Вычислим матрицу АТА. Для этого: – курсор устанавливаем ячейку D21; – вызываем функцию МУМНОЖ; – в качестве «Массив1» указать адрес транспонированной матрицы D11:F13; – в качестве «Массив2» указать адрес матрицы А (D5:F7); – после «Ok» в D21 появится только первый элемент результирующей матрицы (число 9); – для того чтобы увидеть остальные числа: выделяем ячейки D21:F23; нажимаем F2; выполняем тройное нажатие Ctrl + Shift + Enter.
6) Вычислим матрицу ( ATA)–1. Для этого: – курсор устанавливаем ячейку D21; – вызываем функцию МОБР; – в качестве аргумента указать адрес матрицы ATA (D21:F23); – после «Ok» в D26 появится только первый элемент результирующей матрицы (число 0,150); – для того чтобы увидеть остальные числа: выделяем ячейки D26:F28; нажимаем F2; выполняем тройное нажатие Ctrl + Shift + Enter.
7) Вычислим вектор–столбец неизвестных. Для этого: – курсор устанавливаем ячейку D31; – вызываем функцию МУМНОЖ; – в качестве «Массив1» указать адрес матрицы (АТА)–1 (D26:F28); – в качестве «Массив2» указать адрес матрицы АТY (D16:D18); – после «Ok» в D31 появится только первый элемент результирующей матрицы (число –1); – для того чтобы увидеть остальные числа: выделяем ячейки D31:F33; нажимаем F2; выполняем тройное нажатие Ctrl + Shift + Enter.
Таким образом, корни системы (4) равны: x1 = –1; x2 = 2; x3 = 5.
Варианты заданий Решить систему уравнений заданных в виде матриц коэффициентов и свободных членов. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
|

 (2.4)
(2.4)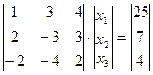 (2.4а)
(2.4а)


