Классификация объектов управления. Алгоритмы их функционирования

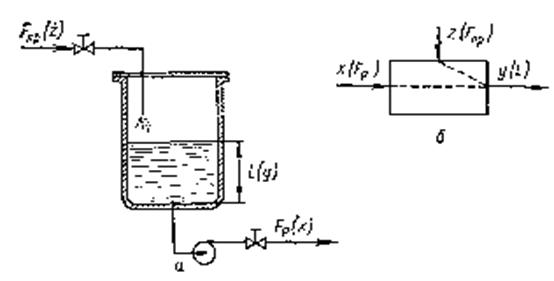
Классификация объектов проводится по ряду признаков.

Одномерные объекты имеют одну выходную величину и описываются одним уравнением статики и одним уравнением динамики. Примером одномерного объекта может служить резервуар для жидкости, входными величинами которого являются приход F_nр и расход F_p жидкости, а выходной величиной — уровень жидкости L.

Увеличение (уменьшение F_nр или F_p вызывает изменение уровня L. Уравнения статики этого объекта имеют вид: L = f (F_nр, F_p), а уравнение динамики – L = f (F_nр, F_p, t).

Многомерные объекты содержат по две, три и более выходных величин. Число уравнений, описывающих состояние, должно соответствовать числу выходных величин. Их выходные величины могут влиять или не влиять одна на другую. В многомерных объектах с независимыми выходными величинами изменение любой из входных величин приводит к изменению только своей выходной величины. Такие объекты можно разбить на несколько одномерных объектов и рассматривать их независимо один от другого.

В многомерных объектах с взаимозависимыми выходными величина ми изменение входных величин приводит к одновременному изменению нескольких выходных величин, что объясняется наличием в таких объектах каналов перекрестных связей.

Объекты с сосредоточенными параметрами – объекты, у которых величины имеют одно числовое значение в данный момент времени во всех точках пространства. Например, аппарат под давлением, - давление во всех точках одинаково. Динамика объектов с сосредоточенными параметрами описывается обыкновенными дифференциальными уравнениями с постоянными коэффициентами, которые дополняются начальными условиями. Такие объекты проще автоматизировать.

Объекты с распределенными параметрами – объекты, регулируемые величины которых имеют разные числовые значения в различных точках объекта в данный момент времени. К ним относится большинство объектов: печи, теплообменники, реакторы и т.д. Один и тот же аппарат, в зависимости от параметра, может обладать свойствами объекта, как с сосредоточенными, так и распределенными параметрами. Динамика объектов с распределенными параметрами описывается дифференциальными уравнениями в частных производных, дополненными начальными и граничными условиями. Т.к. решение уравнений в частных производных более сложно, чем решение обыкновенных дифференциальных уравнений, то при составлении математического описания объектов с распределенными параметрами их часто разбивают на ряд последовательно соединенных элементов с сосредоточенными параметрами, каждый из которых описывается обыкновенным дифференциальным уравнением. Точность такого описания тем выше, чем на большее число элементов был разбит исследуемый объект. Для управления такими объектами используют, как правило, многоконтурные АСР.

В зависимости от вида дифференциального уравнения динамики реального объекта химической технологии различают объекты первого, второго и высших порядков.

Объекты 1-го порядка (одноемкостные). К ним относятся сборники жидкости, бункеры для сыпучих материалов, газовые аккумуляторы, жидкостные смесители, теплообменники смешения и т. д. Во всех этих аппаратах количество вещества или тепла заключено в одном резервуаре. Такие объекты обладают способностью аккумулировать (накапливать) проходящие через них вещество или тепло в переходном режиме. Это выражается в том, что рассогласование потоков на входе и выходе при изменении, например, нагрузки вызывает изменение количества вещества или тепла в объекте, а следовательно, и выходной величины объекта. При этом скорость изменения выходной величины объекта зависит от аккумулирующей способности или инерционных свойств объекта.

Объекты 2-го порядка. В таких объектах вещество или тепло заключено в двух объемах, разделенных сопротивлением. Примерами этих объектов являются теплообменник, в котором тепло передается через стенку от одной жидкости к другой; два сообщающихся между собой сосуда с жидкостью и т. д.

Объекты высшего порядка. С повышением порядка дифференциального уравнения объект реагирует на возмущения все более замедленно. Их поведение в динамике идентично поведению цепочки последовательно соединенных апериодических звеньев первого порядка.

По способности восстанавливать равновесное состояние при конечном изменении входных величин объекты подразделяют на нейтральные, устойчивые и неустойчивые.