Собственные значения и собственные векторы матрицы
Определение. Рассмотрим квадратную матрицу АХ = λ Х. (8) Тогда вектор Определение. Уравнение Определение. Корнем многочлена называется значение переменной, обращающее этот многочлен в нуль. Корнем матричного многочлена будет матрица, обращающая этот многочлен в нулевую матрицу.
Теорема 1. Собственные значения матрицы А Верно и обратное: каждый корень характеристического многочлена матрицы А будет её собственным значением. Теорема 2. Если 1) 2) Эти равенства можно использовать в качестве проверки вычисленных собственных значений. Теорема 3. (Теорема Гамильтона – Кэли). Любая квадратная матрица является корнем своего характеристического многочлена, т. е.
Пример 1. Найти собственные значения матрицы Решение. Чтобы найти собственные значения, приравняем к нулю характеристический многочлен:
Корни квадратного уравнения: Сумма корней Подставим матрицу А в характеристический многочлен:
В результате получили нулевую матрицу. Это и означает, что матрица является корнем своего характеристического многочлена.
Пример 2. Показать, что матрица Решение. ( Найдём характеристический многочлен матрицы:
Вычислим
Тогда
|

 . Пусть для некоторого ненулевого вектора
. Пусть для некоторого ненулевого вектора  и числа l выполняется равенство
и числа l выполняется равенство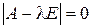 называется характеристическим уравнением.
называется характеристическим уравнением.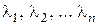 являются корнями характеристического многочлена
являются корнями характеристического многочлена 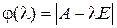 .
.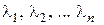 – собственные значения матрицы А, то:
– собственные значения матрицы А, то: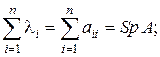
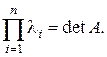
 , где под нулём понимается нулевая матрица, а под свободным членом характеристического многочлена – этот свободный член, умноженный на единичную матрицу.
, где под нулём понимается нулевая матрица, а под свободным членом характеристического многочлена – этот свободный член, умноженный на единичную матрицу.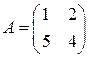 и проверить правильность решения по теореме 3. Проиллюстрировать теорему Гамильтона – Кэли.
и проверить правильность решения по теореме 3. Проиллюстрировать теорему Гамильтона – Кэли.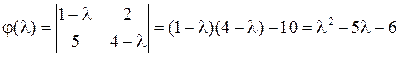 =0.
=0.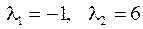 .
.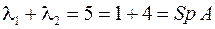 ; произведение корней
; произведение корней 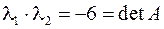 .
.
 .
.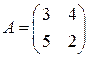 является корнем своего характеристического многочлена.
является корнем своего характеристического многочлена. ;
;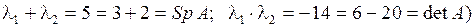 .
.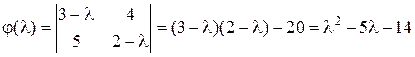 .
.
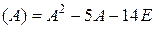 , для этого нужно найти
, для этого нужно найти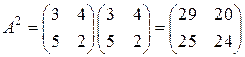 ,
,  и
и  .
.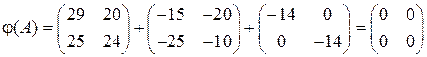 .
.


