Характеристическая матрица и характеристический многочлен
Собственные значения и собственные векторы матрицы
I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Основные вопросы: 1. Характеристическая матрица и характеристический многочлен 2. Собственные значения и собственные векторы матрицы 3. Нахождение собственных векторов
Характеристическая матрица и характеристический многочлен Рассмотрим квадратную матрицу п -го порядка:
Умножим единичную матрицу того же порядка на число l и вычтем её из матрицы А. Определение. Матрица вида
где λ − независимая переменная, называется характеристической матрицей для матрицы А. Определение. Определитель характеристической матрицы (2)
называется характеристическим многочленом матрицы А. Действительно, выражение (3) является многочленом относительно λ, в чём легко убедиться, вычислив определитель любым способом, например, разложением по первой строке. Степень характеристического многочлена матрицы равна порядку этой матрицы, в данном случае эта степень равна n. Определение. Следом матрицы А называется сумма её диагональных элементов:
Найдём характеристические многочлены для квадратных матриц 2-го и 3-го порядков. 1. Для матрицы 2-го порядка
где 2. Для матрицы 3-го порядка
Доказательство. Разложим определитель по первой строке:
=
В общем виде характеристический многочлен можно записать в виде:
Если положить λ = 0, то
Пример 1. Найти характеристический многочлен матрицы Решение.
Пример 2. Найти характеристический многочлен матрицы Решение. Характеристический многочлен найдём, разложив определитель по первой строке:
Проверим правильность вычисления коэффициентов по формуле (6):
|

 . (1)
. (1)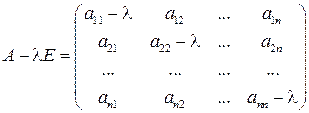 , (2)
, (2)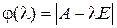 (3)
(3)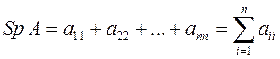 . (4)
. (4)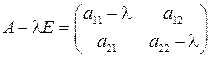 ,
,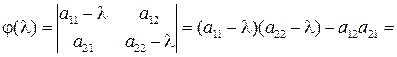
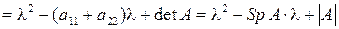 . (5)
. (5)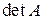 , или
, или 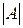 − величина определителя матрицы А.
− величина определителя матрицы А.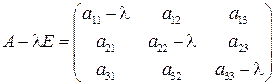 ,
, . (6)
. (6)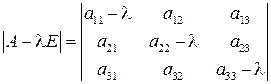 =
= 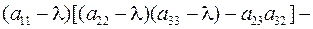
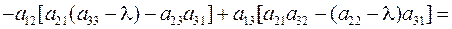
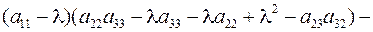
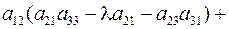
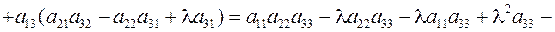
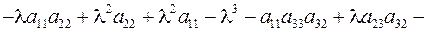
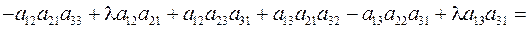
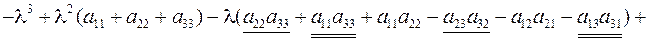
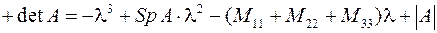 , ч.т.д.
, ч.т.д.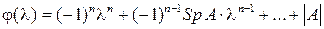 . (7)
. (7)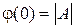 есть свободный член многочлена, равный определителю матрицы А. Это видно и из формулы (2).
есть свободный член многочлена, равный определителю матрицы А. Это видно и из формулы (2).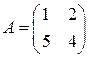 .
.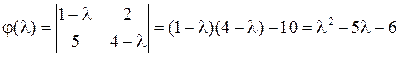 .
.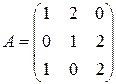 .
.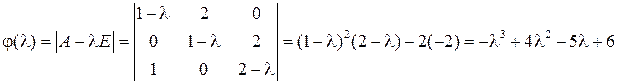 .
.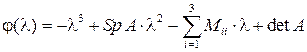 .
.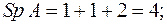
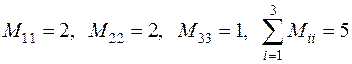 ;
;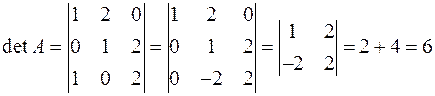 .
.


