Задачи для самостоятельного решения. Найти собственные значения и собственные векторы матрицы А:
Найти собственные значения и собственные векторы матрицы А: 4. 7. 10.
Ответы к задачам 4 – 12: 4. 5. 6. 7. 8. 9. 10. 11. 12.
II. ЛАБОРАТОРНАЯ РАБОТА > restart: Зададим матрицу и определим её тип. > restart: > with(linalg): with(LinearAlgebra):
Найдём характеристическую матрицу:
Характеристический многочлен:
Найдём следы двух матриц:
Найдём её собственные значения и собственные векторы:
> eigenvalues(B);
> eigenvectors(B);
Здесь 5 – первое собственное значение кратности 1. В фигурных скобках находится соответствующий собственный вектор (2,1). Соответственно -1 – это второе собственное значение кратности 1, соответствующий собственный вектор (-1,1). Зададим другую матрицу.
Проделайте с ней те же вычисления. Теперь зададим матрицу 3-го порядка. >
Разложим характеристический многочлен на множители:
Видно, что корнями являются числа 1 (два раза, т.е. кратность этого корня 2) и 2 (кратностью 1). Найдём собственные значения матрицы М, которые и являются корнями характеристического многочлена. Для этого решим уравнение
Можно задать корни в виде списка:
Найдём собственные векторы матрицы М:
Выведен список l, первым элементом которого является столбец собственных значений, а вторым – матрица, строки которой представляют собой соответствующие собственные векторы. Выделим элементы этого списка.
Теперь выделим строки матрицы:
Задание 1. Проделайте те же действия над матрицей ПРОВЕРКА ВЫПОЛНЕНИЯ ТЕОРЕМ 2 И 3 1) Проверим выполнение теоремы 2, т.е. убедимся в том, что сумма собственных значений матрицы М равна её следу, а их произведение равно определителю этой матрицы.
2) Проверим выполнение теоремы 3 (теоремы Гамильтона-Кэли), т.е. убедимся в том, что квадратная матрица М является корнем своего характеристического многочлена. Подставим матрицу М в многочлен ст. Для формирования свободного члена зададим единичную матрицу и умножим её на -2.
Найдём квадрат матрицы М:
Теперь найдём куб:
Составим многочлен в точке М и убедимся в том, что он равен нулю (нулевой матрице).
ЗАДАНИЯ. Найти характеристические матрицы и многочлены следующих матриц: 6) Вычислить их собственные значения и собственные векторы. Проверить выполнение теорем 2 и 3.
|

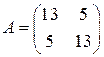 ; 5.
; 5. 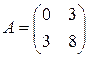 ; 6.
; 6. 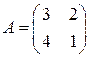 ;
;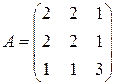 ; 8.
; 8.  ; 9.
; 9. 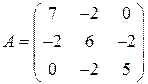 ;
; ; 11.
; 11. 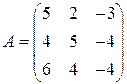 ; 12.
; 12.  .
.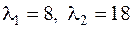 ,
, 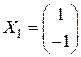 ,
,  .
.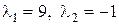 ,
, 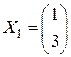 ,
,  .
.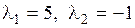 ,
, 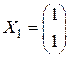 ,
, 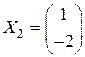 .
.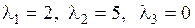 ,
, 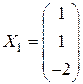 ,
, 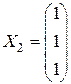 ,
,  .
. ,
, 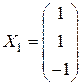 ,
,  ,
, 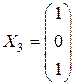 .
.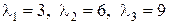 ,
,  ,
, 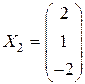 ,
, 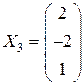 .
.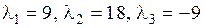 ,
, 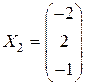 ,
,  .
. ,
, 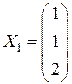 ,
,  ,
,  .
. ,
,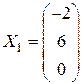 ,
, 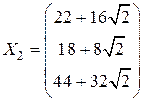 ,
, 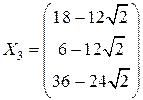 .
.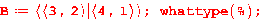
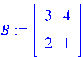

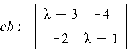



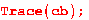
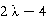

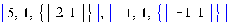

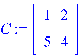

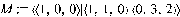
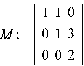

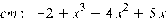
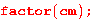






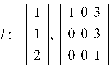

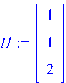


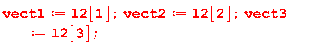
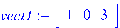
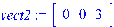
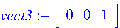
 .
.


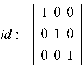


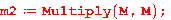

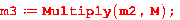
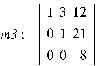

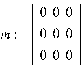
 ; 9)
; 9)  ; 12)
; 12)  .
.


