Идея и основные положения метода перемещений
СОДЕРЖАНИЕ Идея и основные положения метода перемещений................ 2. Матрица жесткости типового элемента плоских рам – балки с защемленными торцами......................................
3. Реакции связей от заданных внешних сил.......................
4. Примеры расчета рам методом перемещений....................
5. Заключительное замечание....................................
6. Литература.................................................
Идея и основные положения метода перемещений
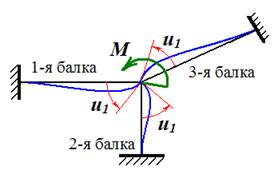
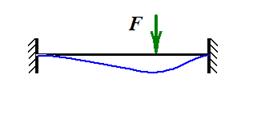
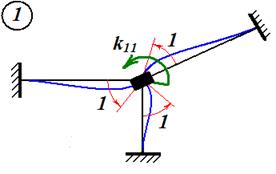
В методе сил в качестве основных неизвестных, через которые выражаются все искомые величины, принимаются или реакции связей, или внутренние силы в некоторых сечениях конструкции. Для расчета сложных (много раз статически неопределимых) систем разработан альтернативный подход, называемый методом перемещений. В методе перемещений за основные неизвестные принимаются перемещения характерных сечений или узлов конструкции. Эти перемещения выбирают так, чтобы через них можно было выразить все искомые величины: деформации, внутренние силы, напряжения во всем объеме конструкции. Рассмотрим идею и технику метода перемещений на примере расчета плоских рам. Так же, как в методе сил, будем пренебрегать изменением длин стержней, считая их нерастяжимыми. Рассмотрим простейший пример (рис.1).
Рис. 1
«Деформированное состояние» рамы определяется одним углом поворота
Рис. 2 Обозначим Используя свойство линейности упругой системы, запишем очевидное уравнение
из которого определяется угол поворота. Верхний индекс у коэффициентов Рассмотренный пример особенно прост потому, что нагрузка приложена к узлу рамы. Рассмотрим чуть более сложную задачу (рис.3). Теперь на раму действует внеузловая нагрузка.
Рис. 3
«Деформированное состояние» каждой балки определяется суперпозицией двух состояний. Первое состояние - это прогибы балки, обусловленные перемещениями ее концевых сечений (в рассматриваемой задаче углом поворота
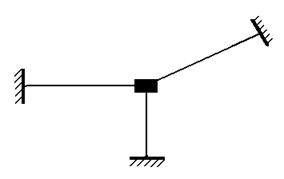
Рис. 4 Возникает вопрос: как формализовать процедуру расчета? Для формализации вводится понятие – основная система метода перемещений. Основная система метода перемещений образуется из заданной путем введения дополнительных связей, устраняющих подвижности узлов. Устраним угол поворота узла рамы, поставив заделку (рис. 5). Эту заделку будем называть «плавающей». «Плавающая» заделка запрещает поворот, не ограничивая линейных перемещений. При необходимости линейные перемещения узлов устраняются путем установки катков.
Рис. 5
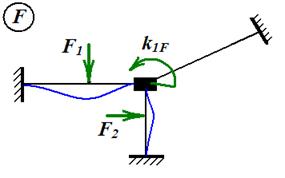
Теперь рама поделена на три балки одного типа - балки с заделками по торцам, которые не взаимодействуют друг с другом. Балку с жестко защемленными торцами будем называть типовым элементом плоских рам. Различные виды деформации типового элемента могут быть изучены заранее до расчета рассматриваемой рамы. Предположим, что вспомогательные задачи о деформациях типового элемента решены. Рассмотрим состояние основной системы под действием внешних сил (рис. 6). Это состояние условно будем называть состоянием F.
Рис. 6
Основываясь на решении задачи, показанной на рис. 4, найдем реактивный момент в дополнительной заделке
где Реакцию дополнительной связи будем считать положительной, если ее направление совпадает с направлением положительного перемещения. Таким образом, положительные направления узловых перемещений и узловых реакций согласованы. Очевидно, что для рамы, показанной на рис. 6, Далее рассмотрим состояние основной системы при повороте плавающей заделки на угол, равный единице (рис. 7). Это состояние назовем 1.
Рис. 7
Вычислим реактивный момент в заделке или, что то же самое, момент, приложенный к узлу для получения «единичного» угла поворота. Этот момент определяется сложением моментов для отдельных балок
В линейно упругих системах внутренние силы и реакции связей пропорциональны перемещениям, поэтому при угле поворота Составим выражение для полного реактивного момента в дополнительной заделке, складывая его значения в двух рассмотренных состояниях. Полный реактивный момент равен нулю, т.к. в действительности дополнительная связь отсутствует
Уравнение (4) называется каноническим уравнением метода перемещений. Еще раз подчеркнем, что смысл этого уравнения – отсутствие реакции дополнительной связи. Иначе говоря, это условие равновесия моментов в узле рамы, выраженное через перемещение. Из уравнения (4) определяется угол поворота Ниже рассматривается более сложная для расчета рама (рис. 8), степень кинематической неопределимости которой равна двум. Искомыми являются углы поворота
Рис. 8
Образуем основную систему метода перемещений (рис.9), запретив повороты путем жесткого защемления узлов.
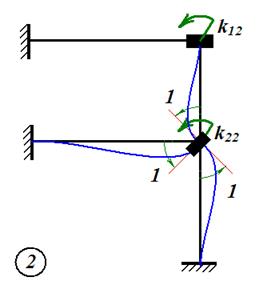
Рис. 9 Чтобы составить канонические уравнения метода перемещений, последовательно рассмотрим три состояния основной системы: · состояние F (рис. 10), возникающее при действии заданных внешних сил; · состояние 1 (рис. 11), возникающее при «единичном» угле поворота первого узла; · состояние 2 (рис. 12), возникающее при «единичном» угле поворота второго узла. Для каждого состояния вычислим реакции дополнительных связей. Реакции сопровождаются двумя индексами. Первый индекс указывает номер дополнительной связи или, что то же самое, номер направления реакции (номер запрещенного узлового перемещения или степени свободы). Второй индекс указывает причину появления реакции. Реакции при действии внешних сил обозначаются
Рис. 10
Рис. 11 Рис. 12
Подчеркнем, что конкретное определение реакций Используя принцип суперпозиции, составим выражения для истинных значений реакций дополнительных связей
Канонические уравнения метода перемещений (5) целесообразно записывать в матричной форме
где Из системы (6) определяются перемещения узлов конструкции. Для формирования уравнений метода перемещений (6) необходимо получить матрицу жесткости для балки с заделками по торцам и определить реакции в заделках при действии внешних сил.
2. Матрица жесткости типового элемента плоских рам – балки с защемленными торцами (рис. 13)
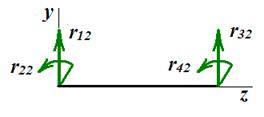
На рис. 14 показаны положительные направления перемещений концевых сечений балки и реакций.
Рассмотрим четыре вида деформации балки и определим реакции в заделках. Реакции (коэффициенты жесткости) типового элемента будем обозначать Первый вид деформации балки (рис. 15). Левому торцу балки сообщается «единичное» линейное перемещение. Искомые реакции показаны на рис. 16. Поскольку реакции обусловлены смещением по направлению 1, то в обозначениях реакций второй индекс – 1.
Рис. 15 Рис. 16 Составим уравнение изогнутой оси балки. Функция изгибающих моментов
кривизна изогнутой оси
углы поворота поперечных сечений
прогибы
Заметим, что при интегрировании были выполнены граничные условия на левом торце балки. Найдем неизвестные реакции
Получаем
Реакции на правом торце найдем из уравнений равновесия балки
Покажем действительные направления реакций и эпюру изгибающих моментов в балке (рис. 17).
Рис. 17
Подставив найденные значения реакций в функцию прогибов, получим ее окончательный вид
где Полученная функция является первым из четырех полиномов Эрмита, широко используемых при интерполяционном представлении функций. В дальнейшем полиномы Эрмита обозначаются
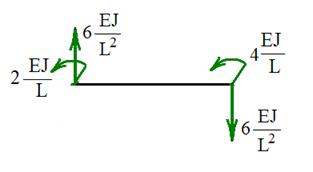
Второй вид деформации балки (рис. 18). Левому торцу балки сообщается «единичное» угловое перемещение. Искомые реакции показаны на рис. 19.
Рис. 18 Рис. 19
Выполняя те же действия, что в первом случае, находим: · изгибающие моменты · кривизну изогнутой оси · углы поворота поперечных сечений · прогибы Удовлетворяя граничные условия на правом торце, получаем значения реакций
Из уравнений равновесия балки
Прогибы балки описываются вторым полиномом Эрмита
Действительные направления реакций и эпюра изгибающих моментов в балке показаны на рис. 20.
Рис. 20
Третий вид деформации балки (рис. 21) повторяет уже рассмотренный случай и не требует детального изучения.
Рис. 21 Рис. 22
Ниже приведены результаты. Реакции
Действительные направления реакций показаны на рис. 23.
Рис. 23 Прогибы балки при третьем виде деформации
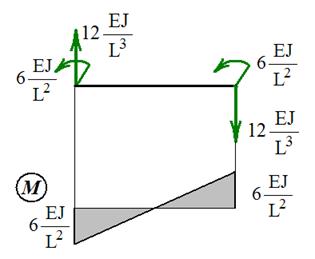
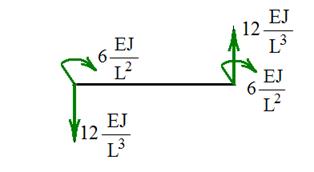
Четвертый вид деформации балки и соответствующие реакции изображены на рис. 24, 25, 26.
Рис. 24 Рис. 25
Рис. 26
Приведем только результаты
Реакции, найденные для всех четырех форм деформации балки, сведем в матрицу жесткости элемента
Составленная матрица жесткости элемента связывает вектор линейных и угловых перемещений
Если внешняя нагрузка приложена в узлах рамы, то для расчета рамы достаточно знать только эту матрицу. В противном случае необходимо определить еще реакции связей от внешней внеузловой нагрузки. Заметим, что матрица жесткости элемента (11) является симметричной по факту построения. Основываясь на принципе взаимности работ, можно доказать свойство симметрии матрицы жесткости любой линейно упругой системы.
|

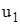 . Если угол поворота
. Если угол поворота 
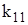 - момент, необходимый для создания единичного угла поворота торца. В дальнейшем коэффициент
- момент, необходимый для создания единичного угла поворота торца. В дальнейшем коэффициент 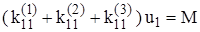 , (1)
, (1)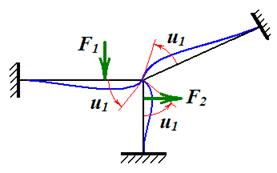
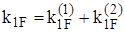 , (2)
, (2)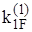 ,
, 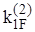 - моменты, возникающие в заделке при нагружении соответственно первой и второй балок.
- моменты, возникающие в заделке при нагружении соответственно первой и второй балок. .
.
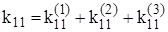 . (3)
. (3)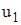 момент составит
момент составит 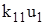 .
.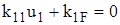 . (4)
. (4) двух узлов рамы.
двух узлов рамы.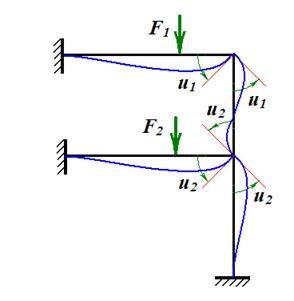
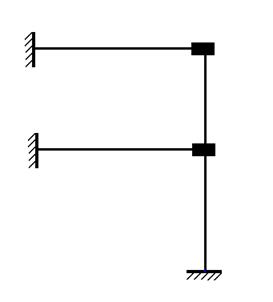
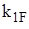 ,
, 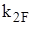 и т.д. Реакции при «единичных» перемещениях узлов обозначаются
и т.д. Реакции при «единичных» перемещениях узлов обозначаются 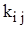 , где индекс j указывает направление «единичного» перемещения. Таким образом,
, где индекс j указывает направление «единичного» перемещения. Таким образом, 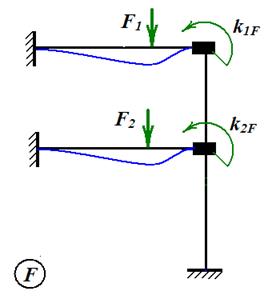

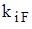 ,
, 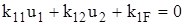 ,
,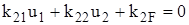 . (5)
. (5)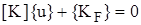 , (6)
, (6)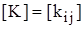 - квадратная матрица жесткости конструкции,
- квадратная матрица жесткости конструкции, 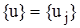 - матрица-столбец (вектор) искомых узловых перемещений,
- матрица-столбец (вектор) искомых узловых перемещений,  матрица-столбец реакций от внешних сил.
матрица-столбец реакций от внешних сил.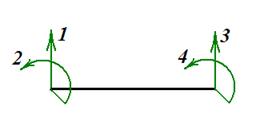

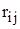 , оставляя обозначение
, оставляя обозначение 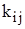 за реакциями в конструкции (раме).
за реакциями в конструкции (раме).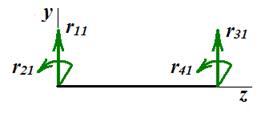
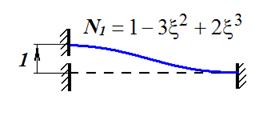
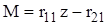 ,
,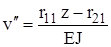 ,
,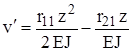 ,
,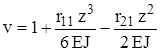 .
.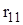 ,
,  , исходя из граничных условий на правом торце
, исходя из граничных условий на правом торце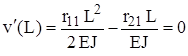 ,
, 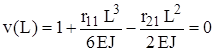 .
.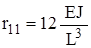 ,
, 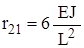 .
.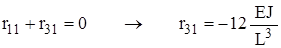 ,
,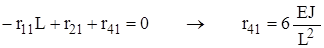 .
.
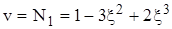 , (7)
, (7)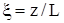 - масштабированная координата поперечного сечения.
- масштабированная координата поперечного сечения.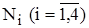 .
.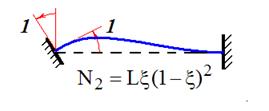
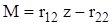 ,
,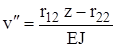 ,
,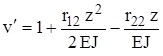 ,
,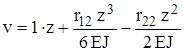 .
.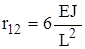 ,
, 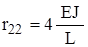 .
.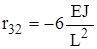 ,
, 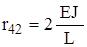 .
.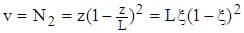 . (8)
. (8)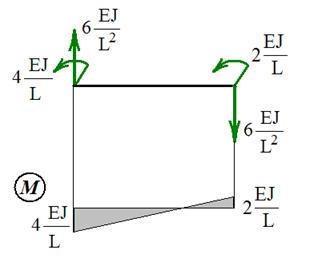
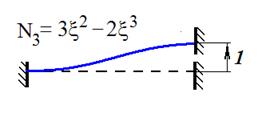

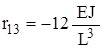 ,
,  ,
, 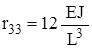 ,
, 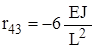 .
.
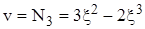 , (9)
, (9)

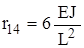 ,
, 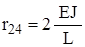 ,
, 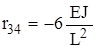 ,
, 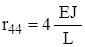 ,
,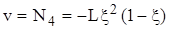 . (10)
. (10) . (11)
. (11)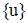 концевых сечений балки с вектором
концевых сечений балки с вектором 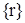 поперечных сил и изгибающих моментов, действующих в тех же сечениях; т.е.
поперечных сил и изгибающих моментов, действующих в тех же сечениях; т.е.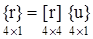 . (12)
. (12)


